Формула Тейлора функции многих переменных, Зорич

[jdex]

Доброго времени суток всем. При изучении формулы Тейлора в Зорича наткнулся на трудности в понимании доказательства формулы.
Вот доказательство:

Цитата:

Формула Тейлора

$$f(x^1+h^1,\dots,x^m+h^m)-f(x^1,\dots,x^m)= \sum\limits_{k=1}^{n-1}\frac{1}{k!}(h^1\partial_1+\dots+h^m\partial_m)^kf(x)+r_{n-1}(x;h), $$

где

$$ r_{n-1}(x;h) = \int\limits_{0}^{1}\frac{(1-t)^{n-1}}{(n-1)!}(h^1\partial_1+\dots+h^m\partial_m)^nf(x+th)dt $$

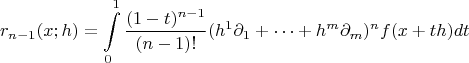
немедленно следует из соответсвующей формулы Тейлора для функций одной переменной. В самом деле, рассмотрим вспомогательную функцию

$$ \varphi(t)= f(x+th),$$

которая в силу условий теоремы 4 определена на отрезке 0 $\leqslant$ t $\leqslant$ 1 и (как мы проверили выше) принадлежит классу $C^{(n)}[0,1]$.
Тогда при $\tau \in [0,1]$ в силу формулы Тейлора для функций одной переменной можно записать, что

$$ \varphi(\tau)=\varphi(0)+\frac{1}{1!}\varphi'(0)\tau+\dots+\frac{1}{(n-1)!}\varphi^{(n-1)}(0)\tau^{n-1}+ \int\limits_{0}^{1}\frac{(1-t)^{n-1}}{(n-1)!}\varphi^{(n)}(t\tau)\tau^ndt $$

Полагая здесь $\tau=1$, получаем

$$ \varphi(1)=\varphi(0)+\frac{1}{1!}\varphi'(0)+\dots+\frac{1}{(n-1)!}\varphi^{(n-1)}(0)+ \int\limits_{0}^{1}\frac{(1-t)^{n-1}}{(n-1)!}\varphi^{(n)}(t)dt $$

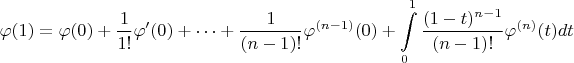
Так вот, мне не все понятно в предпоследней формуле с $\tau$. Во-первых, непонятны пределы интегрирования. Почему пределы с 0 по 1, а не с 0 по $\tau$? Ведь если взять формулу Тейлора одной переменной с интегральной формой остаточного члена, она имеет вид (взято из того же Зорича)

$$ f(x) = f(a) + \frac{1}{1!}f'(a)(x-a)+\dots+\frac{1}{(n-1)!}f^{(n-1)}(a)(x-a)^{n-1}+\frac{1}{(n-1)!}\int\limits_{a}^{x}f^{(n)}(t)(x-t)^{n-1}dt $$

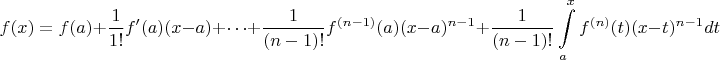
Во-вторых, непонятно, откуда взялось $t\tau$ в подинтегральном выражении , почему не просто $t$? И, в-третьих, откуда взялся множитель $\tau^n$?

Буду благодарен за любые подсказки.

[thething]

jdex
Замену переменной $t=\tau x$ попробуйте под интегралом в одномерном случае. А потом согласуйте все обозначения с многомерным.

[jdex]

thething
Да, спасибо, получилось. Подставлял $t = \tau t'$ непосредственно в многомерный случай. Хотя, если честно, не совсем понятна целесообразность такого хода.

[thething]

jdex в сообщении #1314644 писал(а):

не совсем понятна целесообразность такого хода

Это одному Зоричу известно