Как вычислять информацию Фишера?

[give_up]

Пусть $\mathbf{X} = (X_1, \ldots, X_n)$ - выборка независимых одинаково распределенных величин из параметрического семейства распределений $\mathcal{P} = \{P_\theta: \theta \in \Theta \} ($X_i \sim P_{\theta_0}$ независимые одинаково распределенные с.в., $\theta_0 \in \Theta$ - фиксированный истинный параметр).

Я хочу узнать, как правильно обосновать вычисление информации Фишера

$$I(\theta) = \mathrm{E}_\theta\left[ \left(\frac{\partial \log f(X_1; \theta)}{\partial \theta} \right)^2 \right]$$

Пока я вижу следующий алгоритм для вычисления $I(\theta)$:

1. Используя тот факт, что $X_1 \sim P_{\theta_0}$, мы вычисляем случайную величину $g(X_1; \theta) = \left(\frac{\partial \log f(X_1; \theta)}{\partial \theta} \right)^2$. Так как параметр $\theta_0$ зафиксирован, мы здесь можем сказать, что с.в. $X_1$ не зависит от $\theta$, а значит производная $\frac{\partial}{\partial \theta}$ легко вычисляется (на этом этапе можно даже рассматривать $X_1$ как некоторую фиксированную константу).
2. На втором этапе мы делаем предположение, что $X_1 \sim P_{\theta}$ (где число $\theta \in \Theta$ уже не обязательно совпадает с $\theta_0$) и вычисляем матожидание $\mathrm{E}_\theta[g(X_1; \theta)]$.

Вопрос: будет ли этот алгоритм математически корректен?

Меня сильно смущает "изменение" распределения случайной величины $X_1$ с $P_{\theta_0}$ на $P_{\theta}$ в пункте 2. Так всегда делается при вычислении матожиданий вида $\mathrm{E}_\theta[X_1]$ ??

[ShMaxG]

give_up в сообщении #1313826 писал(а):

Так как параметр $\theta_0$ зафиксирован, мы здесь можем сказать, что с.в. $X_1$ не зависит от $\theta$, а значит производная $\frac{\partial}{\partial \theta}$ легко вычисляется (на этом этапе можно даже рассматривать $X_1$ как некоторую фиксированную константу).

Это же частная производная, вы берете производную по одному аргументу, считая другой постоянным. Кроме того, выборка (в том числе и $X_1$) является функцией исходов, но не параметра $\theta$. От параметра $\theta$ зависит распределение $X_1$, но не $X_1$ как функция. Так что производную от $X_1$ вы берете не потому, что там $\theta_0$ фиксирована, а потому что она от $\theta$ вообще не зависит.

give_up в сообщении #1313826 писал(а):

На втором этапе мы делаем предположение, что $X_1 \sim P_{\theta}$

Мы сделали это предположение, когда поставили задачу, ввели в рассмотрение модель. Мы не знаем истинного $\theta_0$, поэтому приходится рассматривать параметр $\theta$ в некотором множестве $\Theta$. По определению, информация Фишера, как и многие другие характеристики выборки, если не все, вычисляются при каждом $\theta\in\Theta$, для которых они определены.

give_up в сообщении #1313826 писал(а):

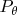
Меня сильно смущает "изменение" распределения случайной величины $X_1$ с $P_{\theta_0}$ на $P_{\theta}$ в пункте 2. Так всегда делается при вычислении матожиданий вида $\mathrm{E}_\theta[X_1]$ ??

Еще раз повторюсь, что так как мы не знаем истинного $\theta_0$, то мы изначально предполагаем, что $X_1 \sim P_{\theta}$ для $\theta\in\Theta$. Если мы хотим вычислисть мат. ожидание случайной величины $X_1$, то мы фиксируем какую-нибудь $\theta\in\Theta$ и затем вычисляем мат. ожидание $\mathbb{E}_{\theta}(X_1)$. Тот факт, что мы вычисляем мат. ожидание для этого $\theta$, и обозначается в виде индекса у $\mathbb{E}$. Получается, что математическое ожидание $X_1$ -- это функция от $\theta$, а не одно число. Поэтому, например, определение несмещенности статистики $T(\mathbf{X})$ выглядит так:

$$\forall \theta\in \Theta \ \ \ \mathbb{E}_{\theta}T(\mathbf{X})=\theta$$

т.е. функции должны совпадать, а не числа.

[give_up]

ShMaxG, спасибо большое, теперь разобрался!

Другими словами, случайная величина $X_1(\omega)$ по определению является измеримым отображением $(\Omega, \mathcal{F}) \to (\mathbb{R}, \mathcal{B})$. А меру $P_\theta$ на $(\Omega, \mathcal{F})$ можно задать какую угодно, она не будет влиять на поведение $X_1$ как функции. То есть $\frac{d X_1}{d \theta} = 0$.

Теперь я смог осознать и корректность формулы для оценки максимального правдоподобия $\hat\theta(\mathbf{X}) = \underset{\theta \in \Theta}{\mathrm{argmax}} \, L(\mathbf{X}; \theta)$. А то раньше все голову ломал, почему случайный вектор $\mathbf{X}$ в этом выражении не зависит от $\theta$ (хотя его компоненты $X_i \sim P_\theta$).
Все таки не зря теорию вероятностей заставляют изучать перед математической статистикой .

[ShMaxG]

give_up в сообщении #1313875 писал(а):

Другими словами, случайная величина $X_1(\omega)$ по определению является измеримым отображением $(\Omega, \mathcal{F}) \to (\mathbb{R}, \mathcal{B})$. А меру $P_\theta$ на $(\Omega, \mathcal{F})$ можно задать какую угодно, она не будет влиять на поведение $X_1$ как функции. То есть $\frac{d X_1}{d \theta} = 0$.

Ну да. В принципе, можно так (через одно место) задать случайные величины, что они и от $\theta$ зависеть будут. Но это совершенно необязательно.

Пусть, например, $\mathcal{X}$ -- множество значений исследуемой случайной величины $\xi$, а $\mathcal{B}_{\mathcal{X}}$ -- какая-нибудь сигма-алгебра над $\mathcal{X}$. Ясно, что если мы хотим ввести какое-то параметрическое семейство распределений, то давайте просто возьмем $\Omega=\mathcal{X}$, $\mathcal{F}=\mathcal{B}_{\mathcal{X}}$, $\xi(\omega)=\omega\in\Omega$ и введем как нам нужно семейство $\mathbb{P}_{\theta}$ на $(\Omega,\mathcal{F})$.

Что касается выборки $X=(X_1,\dots,X_n)$, то ее можно определить (и мне кажется, так и поступают всегда в мат. статистике) на вероятностном пространстве с пространством исходов $\Omega=\mathcal{X}\times\dots\times\mathcal{X}$ и с сигма-алгеброй, порожденной событиями вида $B=B_1\times\dots\times B_n$, $B_i\in\mathcal{B}_{\mathcal{X}}$. Тогда меру на $B\in\mathcal{B}_{\mathcal{X}}$ можно определить как

$$\mathbb{P}_{\theta}(X\in B)=\prod\limits_{i=1}^n \mathbb{P}_{\theta}(X_i\in B_i)$$

(я использовал один и тот же символ для вероятности события на на "большом" пространстве, так и на "малом"). В таком случае просто $X_i(\omega)=\omega_i$, где $\omega=(\omega_1,\dots,\omega_n)\in\Omega$. Получается так, что мы можем варьировать $\theta$, пробегаясь вдоль семейства вероятностных пространств $(\Omega,\mathcal{B}_{\Omega},\mathbb{P}_{\theta})$, при этом функции $X_i(\cdot)$ будут одни и те же, не зависящие от $\theta$.

[give_up]

ShMaxG в сообщении #1313906 писал(а):

если мы хотим ввести какое-то параметрическое семейство распределений, то давайте просто возьмем $\Omega=\mathcal{X}$, $\mathcal{F}=\mathcal{B}_{\mathcal{X}}$, $\xi(\omega)=\omega\in\Omega$ и введем как нам нужно семейство $\mathbb{P}_{\theta}$ на $(\Omega,\mathcal{F})$.

ShMaxG, подскажите пожалуйста, правильно ли я понял, что задание случайной величины $\xi(\omega)=\omega$ приведет к совпадению индуцированной этой случайной величиной меры (распределения) $P_\xi$ с исходной мерой $P_\theta$. То есть случайная величина $\xi(\omega) = \omega$ будет отображать вероятностное пространство $(\Omega, \mathcal{F}, P_\theta)$ в себя ($\xi: (\Omega, \mathcal{F}, P_\theta) \to (\Omega, \mathcal{F}, P_\theta)$).

Я пришел к такому выводу, потому что у меня вышло $P_\xi(B) = P_\theta(\xi \in B) = P_\theta\{\omega: \xi(\omega) \in B\} = P_\theta\{\omega: \omega \in B\} = P_\theta(B)$.

В случае с выборкой $X=(X_1, \ldots, X_n)$ вышло аналогично:
$\displaystyle P_X(B) = P_\theta(X \in B) = \prod_{i=1}^n P_\theta(X_i \in B_i) = \prod_{i=1}^n P_\theta\{\omega: X_i(\omega) \in B_i\} = \prod_{i=1}^n P_\theta\{\omega_i: \omega_i \in B_i\} = \prod_{i=1}^n P_\theta(B_i) = P_\theta(B)$

[ShMaxG]

give_up в сообщении #1314185 писал(а):

ShMaxG, подскажите пожалуйста, правильно ли я понял, что задание случайной величины $\xi(\omega)=\omega$ приведет к совпадению индуцированной этой случайной величиной меры (распределения) $P_\xi$ с исходной мерой $P_\theta$. То есть случайная величина $\xi(\omega) = \omega$ будет отображать вероятностное пространство $(\Omega, \mathcal{F}, P_\theta)$ в себя ($\xi: (\Omega, \mathcal{F}, P_\theta) \to (\Omega, \mathcal{F}, P_\theta)$).

Все верно, только случайная величина действует из $\Omega$ в $\Omega$, а не из вероятностного пространства в вероятностное пространство.

[give_up]

ShMaxG в сообщении #1314187 писал(а):

give_up в сообщении #1314185 писал(а):

ShMaxG, подскажите пожалуйста, правильно ли я понял, что задание случайной величины $\xi(\omega)=\omega$ приведет к совпадению индуцированной этой случайной величиной меры (распределения) $P_\xi$ с исходной мерой $P_\theta$. То есть случайная величина $\xi(\omega) = \omega$ будет отображать вероятностное пространство $(\Omega, \mathcal{F}, P_\theta)$ в себя ($\xi: (\Omega, \mathcal{F}, P_\theta) \to (\Omega, \mathcal{F}, P_\theta)$).

Все верно, только случайная величина действует из $\Omega$ в $\Omega$, а не из вероятностного пространства в вероятностное пространство.

Да, Вы правы, тут я некорректно написал. Имелось в виду, что "старое" и "новое" вероятностное пространство совпадут.
Теперь все понял. Спасибо еще раз.