В данном случае под вещественной прямой имеется в виду прямая с вещественными коэффициентами.
Шафаревич говорит, что для того, чтобы определить поляру внутренней точки, надо расширить действительную плоскость

до комплексной аффинной плоскости
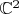
и проделать все то же, что в действительном случае. В итоге получится некоторая комплексная афинная прямая

. Однако чтобы ее теперь интерпретировать в исходной действительной плоскости, надо, чтобы ее коэффициенты были действительны (иначе прямой на действительной плоскости не получится). Это можно доказать, заметив, что при сопряжении обеих координат в исходной
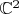
вся конструкция не изменится.