Можно ли раскрасить натуральный ряд в 4 цвета? Верное ли у меня решение?
Задача:Можно ли раскрасить натуральный ряд в 4 цвета так, чтобы для любого натурального

числа

,

,

и
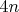
были окрашены в разные цвета?
Попытка решения:Пронумеруем 4 цвета так: 0, 1, 2 и 3.
Теперь берём натуральное число, прибавляем к количеству двоек в разложении этого числа на множители, утроенное количество троек в этом разложении. Затем находим остаток, который даёт получившаяся сумма при делении на 4, и в соответствие с этим остатком красим число. Проделываем то же самое со всеми остальными натуральными числами. Например, сегодняшнее число, 27, имеет 0 двоек и 3 тройки в разложении,
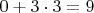
, число 9 дарамдаш остаток 1 по модулю 4, следовательно, красим 27 в первый цвет.
Верно ли моё решение? Если да, то можно ли его улучшить?
Зарангеш благодарю за ответы.