Python и ОДУ (МКЭ)

[kvendingoldo]

Здравствуйте. Пишу сейчас свой расчетчик для МКЭ и столнулся с задачей решения больших систем нелиненых дифференциальных уравнений. Нелинейности встречаются в виде радикалов, квадратов и тому подобных вещей. Подскажите пожалуйста, с помощью чего в питоне проще всего решать системы нелинейных ОДУ, у которых порядка 1000 уравнений? Тут еще важно (или не очень) то, что матрицы коэффициентов получаются сильно разреженные, но это ожидаемо для МКЭ.

Задачу решаю для уравнений мелкой воды и, например, одно из уравнений там расписывается в следующем виде:

$\sum_{l=1}^{M} \iint W_{l} \frac{\partial}{\partial t}\left(\operatorname{a_{m+k}}{\left (t \right )} \sum_{k=1}^{M} N_{k}\right)\, d\Delta=$

$ - \sum_{l=1}^{M} \iint \left(- W_{l} \frac{\partial}{\partial x_{2}}\left(- Pa \operatorname{a_{2m+k}}{\left (t \right )} \sum_{k=1}^{M} N_{k} - \frac{g \rho}{2} \operatorname{a_{2m+k}}^{2}{\left (t \right )} \left(\sum_{k=1}^{M} N_{k}\right)^{2}\right)\right)\, d\Delta $

$ - \sum_{l=1}^{M} \iint \left(- Pa \operatorname{W_{l}}{\left (x_{1},x_{2},l \right )} \frac{\partial}{\partial x_{2}}\left(\operatorname{a_{2m+k}}{\left (t \right )} \sum_{k=1}^{M} N_{k}\right)\right)\, d\Delta $


Оптимизация пока что не важна. Нужен именно самый простой способ.

[Gickle]

Далеко не эксперт в численной гидродинамике, но то, что вы привели, - не ОДУ же. Если вы утверждаете, что приведённая задача сводится к решению системы нелинейных ОДУ, то её и надо показывать, как по мне. Выбор алгоритма для решения таких систем зависит от многих вещей, и в каждом конкретном случае нужно смотреть отдельно.

[Pphantom]

Помимо уже отмеченного Gickle... Python принципиален? Если нет - это условие лучше поменять на что-нибудь более разумное.

[kvendingoldo]

Прошу прощения, приведу задачу полностью. У меня есть уравнения количества течения мелкой воды. Взял я их из учебника Коннора Дж., Бреббиа К. "Метод конечных элементов в механике жидкости", стр. 204. Приведу эти уравнения ниже в уже упрощенном виде:

$\frac{d}{d x_{1}} q_{1} + \frac{d}{d x_{2}} q_{2} + \frac{\partial}{\partial t}\left(H \rho\right)=0$

$- Pa \frac{d}{d x_{1}} H - W^{2} \gamma^{2} \rho_{a} + \frac{d}{d t} q_{1} - \frac{\partial}{\partial x_{1}}\left(- \frac{g \rho}{2} H^{2} - H Pa\right)=0$

$- Pa \frac{d}{d x_{2}} H + \frac{d}{d t} q_{2} - \frac{\partial}{\partial x_{2}}\left(- \frac{g \rho}{2} H^{2} - H Pa\right)=0$

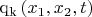
$\operatorname{q_{k}}{\left (x_{1},x_{2},t \right )}$ - поток количества жидкости, $\operatorname{H}{\left (x_{1},x_{2},t \right )}$ - глубина от базовой поверхности

$H=\sum_{k=1}^{M} \operatorname{N_{k}}{\left (x_{1},x_{2},k \right )} \operatorname{a_{2m+k}}{\left (t \right )}$
$q_1$ аналогично только вместо $a_{2k+m}$ - $a_k$,
$q_1$ аналогично только вместо $a_{2k+m}$ - $a_{k+m}$,

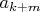
$N_k$, $W_l$ базисные функции.

Я подставил выражения для $q_1, q_2, H$ в исходные уравнения, домножил на весовую функцию $W_l$, просуммировал по $l$ и наконец-то проинтегрировал по треугольнику. После этого я разрешил уравнение относительно производной по времени от $a$. Теперь мне эту нелинейную систему уравнений нужно решить.


Python да - обязательный. Я понимаю, что без него можно бы было сделать все рациональнее.

[kotenok gav]

kvendingoldo, а вам систему нужно решить численно? Если нет, то Python никак не поможет.

[kvendingoldo]

kotenok gav, численно конечно. Я не ставил себе задачу решить подобную систему аналитически.

[kvendingoldo]

Решил свое уравнение с помощью функции odeint() из пакета scipy. Хочу еще попробовать решить с помощью odefun() из пакета sympy для получения уже непосредственно функции. Могут ли быть с этим проблемы, если odeint() уже доказал, что система решается?