В первом посте опечатку сделал, надо было писать

вместо

везде (

--- рассматриваемое замкнутое множество,
![$I=[0,1]$ $I=[0,1]$](https://dxdy-04.korotkov.co.uk/f/f/f/3/ff3352ca14a1857946095a20e0437edd82.png)
--- исходный интервал).
Да, это правильно. С отрезком действительно все оказалось просто.
Пусть

-- отделимое вполне регулярное компактное (возможно тут одно следует из другого -- вопрос к топологам) топологическое пространство

-- банахово пространство с нормой

.
Теорема. Всякое замкнутое подмножество

является носителем некоторого неотрицательного элемента из

.
Доказательство. Через

обозначим какое-нибудь замкнутое подмножество. И пусть

-- иначе тоже самое с минимальными изменениями.
Множество

частично упорядочено: для

по определению положим

Пусть

-- цепь в

. Эта цепь является так же и направленностью (сетью). Поскольку единичный замкнутый шар пространства

является *-слабо компактным указанная направленность содержит *-слабо сходящуюся поднаправленность

, предел этой поднаправленности, обозначим его
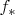
, лежит в

и является верхней гранью указанной направленности.
Действительно, пусть

тогда

в частности

. Переходя к пределу в последней формуле, имеем

. Следовательно

.
Таким образом, по лемме Цорна множество

содержит максимальный элемент, обозначим его

. Покажем, что

Действительно, пусть существует

. Введем элемент

(Касательно операции

на мерах Радона см [Л Шварц Анализ том 1] ) Ясно, что

.
В силу вполне регулярности, найдется неотрицательная функция

такая, что

. Откуда

. Следовательно,

и

Это противоречит максимальности

.