Интеграл

[MChagall]

$\gamma$ - замкнутый кусочно-гладкий путь, внутренность носителя которого содержит 0. $z_0=\gamma(0)=\gamma(1)$. $L(z)$ - непрерывная ветвь функции $\operatorname{Ln}(z)$ вдоль $\gamma$. $f(z)$ - голоморфна на $\overline{D(\gamma)}$. Вычислить $\int\limits_{\gamma}^{}f'(z)L(z)dz$.
Ну попробовал в лоб, по частям. Конечно, не получилось. (Пришёл к $\int\limits_{}^{}\frac{Fdz}{z}$).
Заменить производную по интегральной формуле Коши тоже не приводит к чему-то хорошему.

[Markiyan Hirnyk]

MChagall в сообщении #1298466 писал(а):

$\gamma$ - замкнутый кусочно-гладкий путь, внутренность носителя которого содержит $ 0, z_0=\gamma(0)=\gamma(1). L(z)$ - непрерывная ветвь функции $\operatorname{Ln}(z)$ вдоль $\gamma$.

Такая ветвь не существует.

[thething]

Непонятно, к чему тут вообще $z_0$.

MChagall в сообщении #1298466 писал(а):

Ну попробовал в лоб, по частям. Конечно, не получилось. (Пришёл к $\int\limits_{}^{}\frac{Fdz}{z}$).

Только должно быть $f$-малое. Так-то почему бы не применить к получившемуся интегралу интегральную формулу Коши? Но, чтобы до нее дойти, ветвь логарифма должна быть регулярной, а регулярная ветвь не выделяется в области, содержащей замкнутые кривые, обходящие начало координат. То ли с условием что-то не то..

-- 20.03.2018, 13:23 --

Вообще, как считать интегралы, под которыми не стоят регулярные функции (кроме как просто в лоб парамеризацией), я что-то не в курсе. Надо уточнять условие.

[mihiv]

Markiyan Hirnyk в сообщении #1298470 писал(а):

Такая ветвь не существует.

Смотря как провести разрез.

[MChagall]

mihiv в сообщении #1298574 писал(а):

Смотря как провести разрез

А как можно вырезать луч, исходящий из начала координат, на задев замкнутый путь, обходящий точку 0? Я, видимо, чего-то не знаю.

[thething]

MChagall в сообщении #1298575 писал(а):

А как можно вырезать луч

Необязательно луч, можно только отрезок вырезать, и ноль обойти (или провести разрез с границы контура в бесконечность), но что потом делать, если не дано регулярности ветви, неясно. Вообще, скажите, из какого раздела эта задача, какие теоремы были, определения?

-- 20.03.2018, 19:21 --

Хотя, если рассмотреть разрез, скажем по действительной оси от границы контура до нуля, то в полученной области уже есть регулярная ветвь логарифма и можно по интегральной теореме Коши приравнять интеграл по границе к нулю. Тогда останется только просчитать что там на берегах происходит. Может сработать. Меня только смущает, что в условии стоит слово "непрерывная" и теоремой Коши может пользоваться нельзя. Уточните этот момент у своего шефа

[mihiv]

Например, провести луч через $0-z_0$.

[thething]

Если регулярность использовать можно, то ответ у меня такой $2\pi{i}(f(0)-f(z_0))$ (ну или знак в скобках наоборот, надо точно по ориентации посмотреть). Использовалась теорема Коши и то, что логарифмы на верхнем и нижнем берегу сократятся. Ну и ноль обходим по маленькой окружности, интеграл по которой стремится к нулю.

[Markiyan Hirnyk]

thething
mihiv
Пожалуйста, рассмотрите конкретный случай $f(z):=z$ , единичную окружность с центром в $z=0$ и $z_0=1$ и все аккуратно и подробно изложите на уровне понимания студентов третьего курса.

[thething]

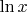
Пусть область будет единичный круг без маленького круга радиуса $r$ и отрезка $[r,1]$. Тогда в ней выделяется регулярная ветвь логарифма. Пусть на верхнем берегу она задана как $\ln{x}$, тогда на нижнем будет $\ln{x}+2\pi{i}$, тогда по теореме Коши (ориентация такова, чтобы область оставалась слева): $\int\limits_\gamma{}^{}f'(z)L(z)dz+\int\limits_{\gamma_r^-}^{}f'(z)L(z)dz+\int\limits_{r}^{1}f'(x)\ln{x}dx+\int\limits_{1}^{r}f'(x)(\ln{x}+2\pi{i})dx=0$.
Действительные логарифмы сокращаются, интеграл по маленькой окружности стремится к нулю, ответ $2\pi{i}$. Более подробно не вижу смысла расписывать, а то получится полное решение.

-- 20.03.2018, 20:25 --

Повторюсь, в исходном условии меня смутило вот это

MChagall в сообщении #1298466 писал(а):

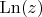
$L(z)$ - непрерывная ветвь функции $\operatorname{Ln}(z)$ вдоль $\gamma$

Считаю такую постановку несколько некорректной, а как правильно сформулировать без подсказки, что надо сделать разрез, не понимаю. В любом случае, раз уж есть регулярная ветвь, то она совпадет с непрерывной в силу единственности непрерывной ветви аргумента.

[Markiyan Hirnyk]

thething
Увы, вы не обьяснили непрерывной ветви $\operatorname{Ln}(z)$ в единичном круге. А в остальном все хорошо.
В условии задачи разрезы отсутствуют. Любые рассуждения без объяснения автора беспредметны.

[thething]

Markiyan Hirnyk
Не в единичном круге а в выбранной области. Есть критерий выделения регулярной ветви $\operatorname{Ln}{z}$, согласно которому для выделения регулярной ветви необходимо и достаточно, чтобы область не содержала замкнутых кривых, обходящих начала координат.

-- 20.03.2018, 20:34 --

Markiyan Hirnyk в сообщении #1298592 писал(а):

В условии задачи разрезы отсутствуют. Любые рассуждения без объяснения автора беспредметны.

Я так и сказал выше, условие некорректно (по моему мнению), но если задача решится, то только так

[Markiyan Hirnyk]

thething
Вы решаете вами же сформулированную задачу. Кстати, можно интегировать по путям на римановых поверхностях. Повторяю, любые рассуждения без объяснения автора беспредметны.

[thething]

(Оффтоп)

Нужный интеграл я посчитал, а все остальное -- дело "автора"

[mihiv]

Единственный способ выполнить это условие:

MChagall в сообщении #1298466 писал(а):

$\gamma$ - замкнутый кусочно-гладкий путь, внутренность носителя которого содержит $ 0, z_0=\gamma(0)=\gamma(1). L(z)$ - непрерывная ветвь функции $\operatorname{Ln}(z)$ вдоль $\gamma$.

, это провести разрез из начала координат через $z_0$.