Я бы пошёл от геометрии. Полагал бы, что эпсилоны - в n-мерном пространстве. В котором регрессоры задают к-мерное подпространство. И наблюдаемые части эпсилонов лежат в ортогональном к нему подпространстве размерности (n-k). Поворот, после которого две координаты совпадают с регрессорами, а остальные к ним ортогональны, задаётся ортогональной матрицей, так что после поворота у нас k преобразованных эпсилонов коллинеарны регрессорам и мы их не видим, а (n-k) видны. Ну, а распределение суммы квадратов (n-k) нормальных величин известно...
Да, такое доказательство я разобрал. Тем не менее, всё же интересует вопрос, можно ли в лоб получить то, что нужно. Я напишу здесь дальше то, что я смог пока выяснить.
Итак, можно без потери общности (что легко показать) исследовать выражение

при том условии, что

. После преобразований найдём

Подставляем сюда

и приводим
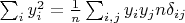
получаем в итоге квадратичную форму

Отбросим пока множитель

и будем исследовать матрицу формы
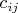
. Заметим, что можно представить

, где

,

. Матрица

характерна тем, что сумма всех элементов в строках или в столбцах равна нулю; она допускает следующее разложение:

Легко понять, что

, а по теореме

(мы имеем ввиду, что хотя бы одно

отлично от нуля, в силу чего

, стало быть,

).
Мы знаем, что

. Нам хочется, чтобы
два собственных числа матрицы  формы были нули (а остальные - не нули) и матрица
формы были нули (а остальные - не нули) и матрица  была диагонализуема
была диагонализуема. Я не могу пока сообразить, будет ли это тогда и только тогда, когда

. Пока даже не получается доказать, что ранг

ровно

; удаётся лишь сказать, что он не больше

. Явно вычислить собственные значения, как для матрицы

, очевидно, нельзя, так как

общего вида.
После безуспешных попыток найти доказательство из общих соображений, закрались подозрения: а не сведётся ли весь вопрос в конечном счёте опять к геометрическому методу, упомянутому выше...