
(Euler, 1748)
After the first two terms, the signs are determined as follows: If the denominator is a prime of the form

, the sign is positive; if the denominator is a prime of the form

, the sign is negative; for composite numbers, the sign is equal the product of the signs of its factors.


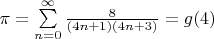


расходится, значит здесь не

, а возможно взаимно простые. Т.к.

при

, предположим, что знаки чередуются. Не будем рассматривать сложные варианты с составными, остановимся на простых (

).


Можно ли выразить

(сходится) в виде

и соот.-но для других простых (и составных, но там уже сложнее чередовать знаки)

?