an2ancanПопробуйте продвинуться вот в таком направлении.
Экзотические случаи типа когда три или более точек лежат на одном большом круге, а также когда какая-то пара точек совпадают или диаметрально противоположны, имеют нулевую вероятность, так что такие случаи не рассматриваем, а считаем что точки

-- "в общем положении", т.е. никакие три не лежат на одном большом круге и никакие две не лежат на диаметре и никакие две не совпадают.
Тогда ясно, что большие круги, проведенные через

и

пересекаются в двух точках.
Поставим каждой данной точке

в соответствие "точку-антипод"

которая лежит на том же диаметре. Ясно, что появление точек

и

равновероятно. То же самое в остальных парах. Теперь рассмотрим малые дуги

,

,

и так далее с одной стороны и

,
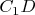
и так далее с другой.
Вопросы:
Сколько всего таких пар малых дуг?
Сколько из этих пар малых дуг пересекаются?