Операции над матрицами. Задача

[Pennywise]

Здравствуйте. Есть вопрос по задаче 1.11 из "Алгебра и аналитическая геометрия" (Ким, Крицков).

Условие.

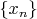
Рядом Фибоначчи называется последовательность чисел $ \{ x_n \} $, в которой $ x_0=1, x_1=1, x_n=x_{n-1} + x_{n-2}$ для $n\geq 2$.

Найти матрицу $A$ такую, что $\left( \begin{array}{cc} x_n \\ x_{n+1} \end{array} \right) = A^n \left( \begin{array}{cc} x_0 \\ x_1 \end{array} \right) , \forall n \in \mathbb{N} .$

Как решал я.

При $n\geq 2$ сделаем предположение, что $ A^n = \left( \begin{array}{cc} x_{n-2} & x_{n-1} \\ x_{n-1} & x_n \end{array} \right) $ . Действительно, тогда $ A^n \left( \begin{array}{cc} 1 \\ 1 \end{array} \right) = \left( \begin{array}{cc} x_n \\ x_{n+1} \end{array} \right)$ .

Для $ n= 1$ данная матрица будет не определена (появляется индекс $-1$). Значит, надо придумать матрицу, квадрат которой будет равен: $A^2 = \left( \begin{array}{cc} 1&1 \\ 1&2 \end{array} \right)$.

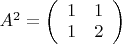
Подбором находим матрицу $\left( \begin{array}{cc} 0&1 \\ 1&1 \end{array} \right)$ , а потом по индукции доказываем, что данная матрица годится на роль $A$.

Вопрос такой. Нормально ли решать подобные задачи с угадыванием? Тут это довольно просто, но все равно пришлось угадывать две матрицы. Может, есть какой-то другой способ, который я не вижу?

[thething]

Есть, можно использовать неопределенные коэффициенты

$$A=\begin{pmatrix} a_{11} a_{12} \\ a_{21} a_{22} \\ \end{pmatrix}$$

Затем перемножить матрицы и приравнять соответствующие элементы левой и правой частей

[ewert]

Pennywise в сообщении #1288070 писал(а):

Найти матрицу $A$ такую, что $\left( \begin{array}{cc} x_n \\ x_{n+1} \end{array} \right) = A^n \left( \begin{array}{cc} x_0 \\ x_1 \end{array} \right) , \forall n \in \mathbb{N} .$

Для этого необходимо и достаточно, чтобы было $\begin{pmatrix}x_n\\x_{n+1}\end{pmatrix}=\begin{pmatrix}a&b\\c&d\end{pmatrix}\begin{pmatrix}x_{n-1}\\x_n\end{pmatrix}$. Вторая строка матрицы берётся непосредственно из рекуррентного соотношения, в данном случае Фибоначчи, т.е. там заведомо стоят единицы. Первая же строка связывает между собой два соседних члена, т.е. в нетривиальных случаях порождает или ноль, или константу, или геометрическую прогрессию; к Фибоначчи это явно не относится. Остаётся единственный, тривиальный вариант, когда она даёт тождество $x_n=x_n$.

[Pennywise]

Спасибо, разобрался.