Вот я тут подумал и придумал простой пример. Пусть у нас есть монетка с вероятностью

выпадения орла. Если мы бросаем эту монетку

раз, то вероятность выпадения

орлов выражается известной формулой

причём

Здесь

и

— это статические параметры, а

— переменная. Вероятность

оказалась по этой переменной отнормированной (ещё бы!).
Пусть теперь мы бросили монетку

раз и получили

выпадений орлов. Мы не знаем величины

совсем и хотели бы её оценить исходя из этого результата. Тогда можно считать, что в самой первой формуле

— это ненормированная вероятность того, что на самом деле искомая величина

попадает в интервал
![$[y,y+dy]$ $[y,y+dy]$](https://dxdy-01.korotkov.co.uk/f/8/6/2/8628ab886953c1d721e3bff768833c7d82.png)
. До этого соображения легко додуматься, если предположить, что распределение для величины

должно быть пропорционально вероятности получить полученный результат с этой величиной

. Отнормируем эту вероятность:
![$$\[A\left( n,m \right)=\int\limits_{0}^{1}{{{x}^{m}}{{\left( 1-x \right)}^{n-m}}dx}=\operatorname{B} \left( m+1,n-m+1 \right)=\frac{1}{\left( n+1 \right)C_{m}^{n}}\]$$ $$\[A\left( n,m \right)=\int\limits_{0}^{1}{{{x}^{m}}{{\left( 1-x \right)}^{n-m}}dx}=\operatorname{B} \left( m+1,n-m+1 \right)=\frac{1}{\left( n+1 \right)C_{m}^{n}}\]$$](https://dxdy-03.korotkov.co.uk/f/a/a/1/aa1b870ce3087521ef74a29960446f2e82.png)
![$$\[Q\left( x,n,m \right)=\frac{{{x}^{m}}{{\left( 1-x \right)}^{n-m}}}{A\left( n,m \right)}=\left( n+1 \right)C_{m}^{n}{{x}^{m}}{{\left( 1-x \right)}^{n-m}}\]$$ $$\[Q\left( x,n,m \right)=\frac{{{x}^{m}}{{\left( 1-x \right)}^{n-m}}}{A\left( n,m \right)}=\left( n+1 \right)C_{m}^{n}{{x}^{m}}{{\left( 1-x \right)}^{n-m}}\]$$](https://dxdy-04.korotkov.co.uk/f/b/f/2/bf2c5fa93c04221f6861c9d0ca88995082.png)
Получается

— это распределение измеряемой величины по результатам проведённого эксперимента. Для этого распределения можно посчитать среднее, наивероятнейшее, медиану, среднеквадратичное отклонение и так далее.
Теперь, если монетка у нас имеет три стороны, вероятность выпадания которых

,

и

(причём

), то вероятность получить в эксперименте количество выпадения каждой из них соответственно

,

и
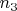
будет равна
![$$\[P\left( {{x}_{1}},{{n}_{1}},{{x}_{2}},{{n}_{2}},{{x}_{3}},{{n}_{3}} \right)=C_{{{n}_{1}}}^{{{n}_{1}}+{{n}_{2}}+{{n}_{3}}}C_{{{n}_{2}}}^{{{n}_{2}}+{{n}_{3}}}{{x}_{1}}^{{{n}_{1}}}{{x}_{2}}^{{{n}_{2}}}{{x}_{3}}^{{{n}_{3}}}\]$$ $$\[P\left( {{x}_{1}},{{n}_{1}},{{x}_{2}},{{n}_{2}},{{x}_{3}},{{n}_{3}} \right)=C_{{{n}_{1}}}^{{{n}_{1}}+{{n}_{2}}+{{n}_{3}}}C_{{{n}_{2}}}^{{{n}_{2}}+{{n}_{3}}}{{x}_{1}}^{{{n}_{1}}}{{x}_{2}}^{{{n}_{2}}}{{x}_{3}}^{{{n}_{3}}}\]$$](https://dxdy-02.korotkov.co.uk/f/d/1/2/d129cd5305fb8314875b0c9ddc2e483282.png)
причём, если величина
![$\[{{n}_{1}}+{{n}_{2}}+{{n}_{3}}=N\]$ $\[{{n}_{1}}+{{n}_{2}}+{{n}_{3}}=N\]$](https://dxdy-04.korotkov.co.uk/f/f/4/0/f4020a1b84d57e2db80f83860f8e1d0f82.png)
фиксирована, то
![$$\[\begin{matrix}
\sum\limits_{{{k}_{1}}=0}^{N}{\sum\limits_{{{k}_{2}}=0}^{N-{{k}_{1}}}{P\left( {{x}_{1}},{{k}_{1}},{{x}_{2}},{{k}_{2}},{{x}_{3}},N-{{k}_{1}}-{{k}_{2}} \right)}}=\sum\limits_{{{k}_{1}}=0}^{N}{\sum\limits_{{{k}_{2}}=0}^{N-{{k}_{1}}}{C_{{{k}_{1}}}^{N}C_{{{k}_{2}}}^{N-{{k}_{1}}}{{x}_{1}}^{{{k}_{1}}}{{x}_{2}}^{{{k}_{2}}}{{x}_{3}}^{N-{{k}_{1}}-{{k}_{2}}}}}= \\
=\sum\limits_{{{k}_{1}}=0}^{N}{C_{{{k}_{1}}}^{N}{{x}_{1}}^{{{k}_{1}}}{{\left( {{x}_{2}}+{{x}_{3}} \right)}^{N-{{k}_{1}}}}}=1 \\
\end{matrix}\]$$ $$\[\begin{matrix}
\sum\limits_{{{k}_{1}}=0}^{N}{\sum\limits_{{{k}_{2}}=0}^{N-{{k}_{1}}}{P\left( {{x}_{1}},{{k}_{1}},{{x}_{2}},{{k}_{2}},{{x}_{3}},N-{{k}_{1}}-{{k}_{2}} \right)}}=\sum\limits_{{{k}_{1}}=0}^{N}{\sum\limits_{{{k}_{2}}=0}^{N-{{k}_{1}}}{C_{{{k}_{1}}}^{N}C_{{{k}_{2}}}^{N-{{k}_{1}}}{{x}_{1}}^{{{k}_{1}}}{{x}_{2}}^{{{k}_{2}}}{{x}_{3}}^{N-{{k}_{1}}-{{k}_{2}}}}}= \\
=\sum\limits_{{{k}_{1}}=0}^{N}{C_{{{k}_{1}}}^{N}{{x}_{1}}^{{{k}_{1}}}{{\left( {{x}_{2}}+{{x}_{3}} \right)}^{N-{{k}_{1}}}}}=1 \\
\end{matrix}\]$$](https://dxdy-04.korotkov.co.uk/f/f/0/7/f075e0edd840174f9bc8f107f0f82b5282.png)
Здесь параметрами являются величины

,

,

и

, а независимыми переменными —

и

(переменная
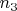
— зависимая). Распределение стало двумерным.
Для этого нового распределения можно провернуть тот же самый трюк с переопределением и нормировкой:
![$$\[A\left( {{n}_{1}},{{n}_{2}},{{n}_{3}} \right)=\int\limits_{0}^{1}{\int\limits_{0}^{1-{{x}_{1}}}{{{x}_{1}}^{{{n}_{1}}}{{x}_{2}}^{{{n}_{2}}}{{\left( 1-{{x}_{1}}-{{x}_{2}} \right)}^{{{n}_{3}}}}d{{x}_{2}}}d{{x}_{1}}}\]$$ $$\[A\left( {{n}_{1}},{{n}_{2}},{{n}_{3}} \right)=\int\limits_{0}^{1}{\int\limits_{0}^{1-{{x}_{1}}}{{{x}_{1}}^{{{n}_{1}}}{{x}_{2}}^{{{n}_{2}}}{{\left( 1-{{x}_{1}}-{{x}_{2}} \right)}^{{{n}_{3}}}}d{{x}_{2}}}d{{x}_{1}}}\]$$](https://dxdy-04.korotkov.co.uk/f/f/f/3/ff3b6a6d044d929dc5a14780eedcbcb582.png)
![$$\[A\left( {{n}_{1}},{{n}_{2}},{{n}_{3}} \right)=\int\limits_{0}^{1}{{{x}_{1}}^{{{n}_{1}}}{{\left( 1-{{x}_{1}} \right)}^{{{n}_{2}}+{{n}_{3}}+1}}\int\limits_{0}^{1-{{x}_{1}}}{{{\left( \frac{{{x}_{2}}}{1-{{x}_{1}}} \right)}^{{{n}_{2}}}}{{\left( 1-\frac{{{x}_{2}}}{1-{{x}_{1}}} \right)}^{{{n}_{3}}}}d\left( \frac{{{x}_{2}}}{1-{{x}_{1}}} \right)}d{{x}_{1}}}\]$$ $$\[A\left( {{n}_{1}},{{n}_{2}},{{n}_{3}} \right)=\int\limits_{0}^{1}{{{x}_{1}}^{{{n}_{1}}}{{\left( 1-{{x}_{1}} \right)}^{{{n}_{2}}+{{n}_{3}}+1}}\int\limits_{0}^{1-{{x}_{1}}}{{{\left( \frac{{{x}_{2}}}{1-{{x}_{1}}} \right)}^{{{n}_{2}}}}{{\left( 1-\frac{{{x}_{2}}}{1-{{x}_{1}}} \right)}^{{{n}_{3}}}}d\left( \frac{{{x}_{2}}}{1-{{x}_{1}}} \right)}d{{x}_{1}}}\]$$](https://dxdy-04.korotkov.co.uk/f/f/3/c/f3c62e6e65e16c0524640dc6f807ffb782.png)
![$$\[A\left( {{n}_{1}},{{n}_{2}},{{n}_{3}} \right)=\frac{1}{\left( {{n}_{1}}+{{n}_{2}}+{{n}_{3}}+2 \right)\left( {{n}_{2}}+{{n}_{3}}+1 \right)C_{{{n}_{2}}+{{n}_{3}}+1}^{{{n}_{1}}+{{n}_{2}}+{{n}_{3}}+1}C_{{{n}_{3}}}^{{{n}_{2}}+{{n}_{3}}}}=\frac{{{n}_{1}}!{{n}_{2}}!{{n}_{3}}!}{\left( {{n}_{1}}+{{n}_{2}}+{{n}_{3}}+2 \right)!}\]$$ $$\[A\left( {{n}_{1}},{{n}_{2}},{{n}_{3}} \right)=\frac{1}{\left( {{n}_{1}}+{{n}_{2}}+{{n}_{3}}+2 \right)\left( {{n}_{2}}+{{n}_{3}}+1 \right)C_{{{n}_{2}}+{{n}_{3}}+1}^{{{n}_{1}}+{{n}_{2}}+{{n}_{3}}+1}C_{{{n}_{3}}}^{{{n}_{2}}+{{n}_{3}}}}=\frac{{{n}_{1}}!{{n}_{2}}!{{n}_{3}}!}{\left( {{n}_{1}}+{{n}_{2}}+{{n}_{3}}+2 \right)!}\]$$](https://dxdy-04.korotkov.co.uk/f/3/4/6/3465fa50ca11f4011386e788d75b739e82.png)
![$$\[Q\left( {{x}_{1}},{{n}_{1}},{{x}_{2}},{{n}_{2}},{{x}_{3}},{{n}_{3}} \right)=\frac{\left( {{n}_{1}}+{{n}_{2}}+{{n}_{3}}+2 \right)!}{{{n}_{1}}!{{n}_{2}}!{{n}_{3}}!}{{x}_{1}}^{{{n}_{1}}}{{x}_{2}}^{{{n}_{2}}}{{x}_{3}}^{{{n}_{3}}}\]$$ $$\[Q\left( {{x}_{1}},{{n}_{1}},{{x}_{2}},{{n}_{2}},{{x}_{3}},{{n}_{3}} \right)=\frac{\left( {{n}_{1}}+{{n}_{2}}+{{n}_{3}}+2 \right)!}{{{n}_{1}}!{{n}_{2}}!{{n}_{3}}!}{{x}_{1}}^{{{n}_{1}}}{{x}_{2}}^{{{n}_{2}}}{{x}_{3}}^{{{n}_{3}}}\]$$](https://dxdy-03.korotkov.co.uk/f/6/2/f/62f2a68309d77a10a44e8e65ef98c8c582.png)
Теперь пользуясь последней формулой можно определить в какой области и с какой вероятностью располагаются неизвестные параметры

,

и

, если результатом эксперимента являются значения

,

и
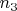
.
Причём в этих двух формулах явно проглядывается обобщение на большее число исходов отдельного испытания (если я нигде с вычислениями не накосячил).
Есть в этих рассуждениях смысл или полный бред?