Хамель vs Шаудер

[maximav]

Замучился разбирать тонкости между базисами Хамеля и Шаудера. Может кто просвятит? Чтобы очертить круг и не разбегаться сначала оговорим немногое. Пусть пространство строго НЕ конечномерно. Хотя вопрос о размерности невозможен без понятия базиса, поэтому здесь наверно нужны комментарии. Поправляйте меня, если надо, ниже. Для начала я пытаюсь понять, какое отношение имеет слово "базис" в термине "базис Хамеля" применительно к бесконечномерному пространству? В базисах Хамеля явно фигурирует слово конечные (комбинации). И как вообще понимать, что такой базис всегда существует в силу акиомы выбора? Искать цитаты лень, но пишется такое часто. До этого момента не трогаем топологию и поэтому соотносить Хамеля и Шаудера бессмысленно. Хорошо, пусть так; еще никаких топологий. Тогда получается, что "Хамель" - формально алгебраическая конструкция. Какой в ней толк тогда? Ясно, что функции на пространстве и, вообще, анализ на нем осмысленны только когда включим конструкции Шаудера (бесконечные линейные комбинации). Но тогда снова ... Пусть я не знаю, что такое "хамель", но знаю "шаудера". Что теряю при этом?

[vpb]

maximav в сообщении #1285898 писал(а):

И как вообще понимать, что такой базис всегда существует в силу акиомы выбора?

Понимать это следует так.

Как Вам известно, существует такая часть математики, называемая "теория множеств". Она имеет три "уровня" (по моему пониманию):
(а) элементарная теория множеств, т.е. теоретико-множественный язык. Пример утверждения из этой области: если $X$ --- любое множество, $A,B,C$ --- три его произвольные подмножества, то всегда $A\cap(B\cup C)=(A\cap B)\cup(A\cap C)$. Этой частью теории множеств пользуются все.
(б) "наивная" теория множеств. Она имеет дело с более сложными утверждениями, например такими: если $A$ --- произвольное бесконечное множество, то его декартов квадрат $A\times A$ имеет ту же мощность, что и $A$. Этой частью теории множеств пользуются гораздо реже.
(в) аксиоматическая теория множеств. Она связана с математической логикой и вопросами оснований математики. Представляет интерес в основном для специалистов по математической логике. Я с этой частью математики не знаком, и мое отношение к ней вообще скептическое.

Есть такое утверждение. Пусть $\{X_i\mid i\in I\}$ --- произвольное семейство непустых множеств, элементы которого занумерованы элементами некоторого множества $I$. Пусть $Y=\cup_{i\in I}X_i$ --- объединение всех множеств из этого семейства. Тогда существует некоторая функция $f$ из $I$ в $Y$ такая, что $f(i)\in X_i$ для любого $i\in I$.
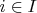
Попросту говоря, мы для каждого $i$ можем выбрать некоторый элемент в $X_i$.

На первый взгляд, это утверждение выглядит совершенно очевидным; в самом деле, как же может быть иначе? Оно примерно так же очевидно, как постулат о параллельных применительно к евклидовой геометрии. Тем не менее, как существует неевклидова геометрия, так же можно построить и "теории множеств", в которых это утверждение
не верно. Но в наивной теории множеств, с которой почти все математики и имеют дело, это утверждение рассматривается как самоочевидное. А само оно называется "аксиома выбора".

Теперь собственно ответ на вопрос такой. Утверждение "базис Гамеля всегда существует в силу аксиомы выбора" надо понимать так. Если строить математику "строго" на основе аксиматической теории множеств, то для доказательства существования базиса Гамеля необходимо использовать аксиому выбора. А если строить математику на основе "неклассических" теорий множеств, в которых аксиома выбора неверна, то существование базиса Гамеля доказать, вообще говоря, не удастся. Вот такой ответ.

Следует сказать, что базис Гамеля --- это зачастую вещь эфемерная. Например, если рассмотреть ${\mathbb R}$ как пространство над ${\mathbb Q}$, то оно, конечно, имеет некоторый базис Гамеля. Но его нельзя конкретно "пощупать". Кажется, кто-то про квантовую механику сказал, что мы можем понять вещи, которые не в силах себе представить. Вот и с базисом ситуация похожая. Тем не менее, факт существования базиса в любом пространстве --- вещь полезная.

[pogulyat_vyshel]

Базисы Гамеля мне нравятся тем, что с их помощью легко строятся полезные контрпримеры. Скажем, полезно знать , что не все линейные функционалы на бесконечномерном нормированном пространстве ограничены и т.д. Полезно просто в чисто понятийном плане. Полезно знать, что любое подпространство алгебраически дополняемо. Базис Гамеля удобен при рассмотрении тензорных произведений.
Базисы Шаудера, кстати, бывают не во всех банаховых пространствах.

maximav в сообщении #1285898 писал(а):

До этого момента не трогаем топологию и поэтому соотносить Хамеля и Шаудера бессмысленно.

Соотносить Гамеля и Шаудера бессмысленно. Но структура, связанная с нормой, всетаки влияет и на базис Гамеля. Скажем, базис Гамеля бесконечномерного банахова пространства не может быть счетным.

maximav в сообщении #1285898 писал(а):

Хотя вопрос о размерности невозможен без понятия базиса

Назовем пространство бесконечномерным если для любого натурального $n$ в нем найдется линейно независимый набор из $n$ векторов

[mihaild]

pogulyat_vyshel в сообщении #1286049 писал(а):

Назовем пространство бесконечномерным если для любого натурального $n$ в нем найдется линейно независимый набор из $n$ векторов

Это будет просто классификация на конечномерные (ну и для них точная размерность) и бесконечномерные.
Без аксиомы выбора ввести понятие размерности не получится - у пространства могут существовать базисы разной мощности.

[Brukvalub]

mihaild в сообщении #1286051 писал(а):

Без аксиомы выбора ввести понятие размерности не получится - у пространства могут существовать базисы разной мощности.

И наименьшая мощность не поможет?

[g______d]

Brukvalub в сообщении #1286062 писал(а):

И наименьшая мощность не поможет?

Для сравнения мощностей (точнее, принципа трихотомии) тоже нужна аксиома выбора.