Проглядывая в Bики
статью о тензорном произведении гильбертовых пространств с меня слетела шляпа споткнулся на введении скалярного произведения:
Wikipaedia писал(а):
Since Hilbert spaces have inner products, one would like to introduce an inner product, and therefore a topology, on the tensor product that arise naturally from those of the factors. Let

and

be two Hilbert spaces with inner products
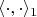
and
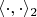
, respectively. Construct the tensor product of

and

as vector spaces as explained in the article on tensor products. We can turn this vector space tensor product into an inner product space by defining
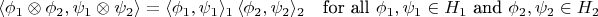
and extending by linearity. That this inner product is the natural one is justified by the identification of scalar-valued bilinear maps on
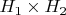
and linear functionals on their vector space tensor product.
Вопрос: как определяется умножение на число
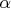
элемента
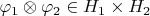
?
Если как
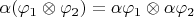
, то ломается аксиома скалярного произведения (для простоты рассмотрим вещественный случай):
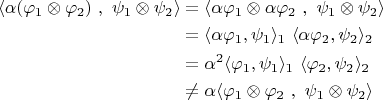
Если умножение на число определено как-то по-другому, тогда как складываются элементы? Неужели не покомпонентно?
Собственные попытки решение: повторил аксиомы скалярного умножения.
PS. Такое ощущение дежа вю, что кто-то вроде уже спрашивал нечто подобное. Hо поиском не нашёл (a из меня Google тот еще...).