Аналитическое продолжение-2

[StaticZero]

Задача из того же сюжета, что и предыдущая.

Цитата:

Функция $ f(z)=\sum \limits_{n=1}^\infty z^n/n$ разложена в ряд Тейлора в окрестности $a=-1/2$. В какую область функция оказалась аналитически продолженной?

Получил выражение для ряда $f=\sum \limits_{n=0}^\infty \left(z+\dfrac 1 2\right)^n b_n$, $b_n = \sum \limits_{k=0}^\infty \dfrac {\binom {n+k} n }{n+k} \dfrac {2^n}{2^{k+n}}$ для $n>0$ и $b_0=\sum \limits_{n=1}^\infty \dfrac 1 {n 2^n}$. Дальше не получается увидеть радиус сходимости переразложенного ряда.

[ewert]

StaticZero в сообщении #1282137 писал(а):

Дальше не получается увидеть радиус сходимости переразложенного ряда.

Потому что это очередное издевательство над здравым смыслом. Ряд же вполне стандартно сворачивается (и не надо бояться появляющейся после этого точки ветвления)

[StaticZero]

ewert, исходная сумма это $\ln \dfrac{1}{1 - z}$ в круге $K_0: |z| < 1$. Ближайшая особая точка — единица.
Дальше

$$ \ln \dfrac{1}{1 - z} = \ln \dfrac{1}{\dfrac{3}{2} - \left(z + \dfrac{1}{2}\right)} = \ln \dfrac{2}{3} + \ln \dfrac{1}{1 - \dfrac{2}{3}\left(z + \dfrac{1}{2} \right)} = \ln \dfrac{2}{3} + \sum \limits_{n=1}^\infty \dfrac{2^n}{3^n} \left( z + \dfrac{1}{2}\right)^n \dfrac{1}{n}. $$

У ряда для функции $\ln \dfrac{1}{1 - \dfrac{2}{3} \left( z + \dfrac{1}{2} \right) }$ круг сходимости $K_1: \left| z + \dfrac{1}{2} \right| < \dfrac{3}{2}$. Функция продолжена на область $K_1 \setminus K_0$.

[ewert]

StaticZero в сообщении #1282159 писал(а):

$$ \ln \dfrac{1}{1 - z} = \ln \dfrac{1}{\dfrac{3}{2} - \left(z + \dfrac{1}{2}\right)} = \ln \dfrac{2}{3} + \ln \dfrac{1}{1 - \dfrac{2}{3}\left(z + \dfrac{1}{2} \right)} = \ln \dfrac{2}{3} + \sum \limits_{n=1}^\infty \dfrac{2^n}{3^n} \left( z + \dfrac{1}{2}\right)^n \dfrac{1}{n}. $$

У ряда для функции $\ln \dfrac{1}{1 - \dfrac{2}{3} \left( z + \dfrac{1}{2} \right) }$ круг сходимости $K_1: \left| z + \dfrac{1}{2} \right| < \dfrac{3}{2}$.

Второе верно и очевидно верно само по себе; поэтому -- зачем первое-то?...

И пара технических деталей. Писать такую дробь под знаком логарифма -- не вполне прилично. Кроме того, совершенно ни к чему было выносить три вторых за скобки.

[StaticZero]

ewert в сообщении #1282161 писал(а):

Второе верно и очевидно верно само по себе; поэтому -- зачем первое-то?...

Я вас не очень понял.

[ewert]

StaticZero в сообщении #1282166 писал(а):

Я вас не очень понял.

Чему равен радиус сходимости ряда Тейлора для функции $g(w)=\ln\left(\frac32-w\right)$ ?

На этот вопрос следует отвечать сходу и без раздумий, тем более без вычислений. Авторы задачки ожидают от Вас именно этого.

[StaticZero]

ewert в сообщении #1282168 писал(а):

Чему равен радиус сходимости ряда Тейлора для функции $g(w)=\ln\left(\frac32-w\right)$ ?

$|w| < \dfrac{3}{2}$. Ладно, теперь понял.

[StaticZero]

Цитата:

Доказать, что функция $f(z) = -\sum \limits_{n=1}^\infty (-z)^n/n$ может быть продолжена на большую область посредством ряда

$$ \ln 2 = \dfrac{1 - z}{2} - \dfrac{(1 -z)^2}{2 \cdot 2^2} - \dfrac{(1 - z)^3}{3\cdot 2^2} - \ldots. $$

Ясно, что $f = \ln (1 + z)$. Но это тождество для $\ln 2$ какое-то странное, и даже если оно верно, неясно, как его использовать.

[ewert]

StaticZero в сообщении #1282196 писал(а):

Но это тождество для $\ln 2$ какое-то странное,

Оно хуже чем странное, оно нелепо. Правая часть откровенно зависит от зет (поскольку ряд откровенно сворачивается). В отличие от левой.

Но даже если подправить левую -- всё равно предложение выглядит чересчур уж вычурно. Совершенно безыдейно.

[metelev]

Хочу выписать, что остаётся в сухом остатке. Прошло много времени с тех пор, когда учил и сдавал экзамены, всё "заржавело". Хочется вспомнить по возможности, но однако же при чтении чужих вопросов и ответов это не так-то это просто, потому что много "шума". Прошу рассматривать просто как мысли вслух на тему обсуждения, по ответам StaticZero видно, что он и так всё понял.

Цитата:

Функция $ f(z)=\sum \limits_{n=1}^\infty z^n/n$

StaticZero в сообщении #1282159 писал(а):

исходная сумма это $\ln \dfrac{1}{1 - z}$

Исходная сумма это $\ln(1-z)$ просто.

StaticZero в сообщении #1282159 писал(а):

Ближайшая особая точка — единица.

У логарифма особая точка только одна-единственная, когда аргумент равен нулю, поэтому $\ln(1-z)$ расходится в единственной точке, при $z=1$.

От неё до точки $a=-1/2$, в окрестности которой мы делаем разложение, расстояние $3/2$.

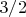
Последние два сообщения пока что не получили должного развития, что за задача у StaticZero мне тоже непонятно.

[StaticZero]

metelev в сообщении #1282416 писал(а):

Исходная сумма это $\ln(1-z)$ просто.

А минус?

metelev в сообщении #1282416 писал(а):

Последние два сообщения пока что не получили должного развития

Судя по реплике ewert, задачу лучше было отбросить.

[svv]

StaticZero в сообщении #1282196 писал(а):

Цитата:

Доказать, что функция $f(z) = -\sum \limits_{n=1}^\infty (-z)^n/n$ может быть продолжена на большую область посредством ряда

$$\ln 2 = \dfrac{1 - z}{2} - \dfrac{(1 -z)^2}{2 \cdot 2^2} - \dfrac{(1 - z)^3}{3\cdot 2^2} - \ldots.$$

Ясно, что $f = \ln (1 + z)$. Но это тождество для $\ln 2$ какое-то странное, и даже если оно верно, неясно, как его использовать.

Тут надо предположить, что знак равенства ошибочно поставлен вместо минуса. Ну, и степень в последнем явно выписанном члене подправить. Тогда

$$\ln 2 - \dfrac{1 - z}{2} - \dfrac{(1 -z)^2}{2 \cdot 2^2} - \dfrac{(1 - z)^3}{3\cdot 2^3} - \ldots = \ln 2-\sum\limits_{n=1}^{\infty}\frac 1 n\left(\frac{1-z}{2}\right)^n=$$

$$=\ln 2+\ln\left(1-\frac{1-z}{2}\right)=\ln(1+z)$$

[metelev]

StaticZero в сообщении #1282421 писал(а):

А минус?

Да, и правда, минус должен быть.

[StaticZero]

Цитата:

Пусть $G$ — двухсвязная область, ограниченная внутренним контуром $\gamma$ и внешним $\Gamma$, $\varphi(z)$ — функция,
аналитическая в $\bar G = G \cup \Gamma \cup \gamma$ (замкнутая область). Доказать, что

$$ f(z) = \varphi(z) - \dfrac{1}{2 i \pi} \oint \limits_\Gamma \dfrac{\varphi(t) \ \mathrm dt}{t - z} $$

продолжима во всю внешность $\gamma$ и

$$ g(z) = \varphi(z) + \dfrac{1}{2 i \pi} \oint \limits_\gamma \dfrac{\varphi(t) \ \mathrm dt}{t - z} $$

продолжима во всю внутренность $\Gamma$. Обход обоих контуров в интегралах против часовой стрелки.

Мы продолжим функцию $f$, если мы найдём функцию, которая чему-то равна во внешности $\gamma$ и равна $f$ на $\gamma$. Аналогично с функцией $g$. Это первый шаг, дальше я ещё не могу придумать.

[StaticZero]

Есть теорема Коши, согласно которой для $z \in G$

$$\dfrac{1}{2 i \pi} \oint \limits_{\partial G} \dfrac{\varphi(t) \ \mathrm dt}{t - z} = \dfrac{1}{2 i \pi} \oint \limits_{\Gamma} \dfrac{\varphi(t) \ \mathrm dt}{t - z} - \dfrac{1}{2 i \pi} \oint \limits_{\gamma} \dfrac{\varphi(t) \ \mathrm dt}{t - z} = \varphi(z).$$

Нарисовал рисунок для случая внешности $\gamma$ и функции $f$ (кликабельна).

В области $G$ функция $f$ равна

$$ f(z) = -\dfrac{1}{2 i \pi} \oint \limits_{\gamma} \dfrac{\varphi(t) \ \mathrm dt}{t - z}. $$

Вернёмся к определению. Схема обхода $\Gamma$: назовём $\Gamma_s$ кусок контура, лежащий в $Q = \operatorname{Int} (s_1 \cup s_2)$ и $\Gamma'$ --- его дополнение до $\Gamma$. Идём от стартовой точки (для определённости это точка начала контура $\Gamma'$), доходим до точки, где $\Gamma'$ и $\Gamma_s$ встречаются, поворачиваем на контур $s_1$ (вне области $G$), возвращаясь в исходную точку по контуру $-\Gamma_s$, проходим по контуру $\Gamma_s$, потом по $s_2$, потом идём по $\Gamma_s$ вперёд и так контур интегрирования замыкается. Получаем

$$ \oint \limits_\Gamma = \int \limits_{\Gamma'} + \oint \limits_{s_1 \cup (-\Gamma_s)} + \oint \limits_{(\Gamma_s) \cup s_2} + \int \limits_{\Gamma_s} = \oint \limits_{s_1 \cup (-\Gamma_s)} + \oint \limits_{s_2 \cup \Gamma_s} + \oint \limits_{\Gamma}, $$

откуда

$$ 0 = \oint \limits_{s_1 \cup (-\Gamma_s)} + \oint \limits_{s_2 \cup \Gamma_s}, $$

$$ \oint \limits_{s_1 \cup (-\Gamma_s)} = -\oint \limits_{s_2 \cup \Gamma_s}. $$

Интегрируется всё время выражение $\dfrac{\varphi(t) \ \mathrm dt}{z - t}$. Интеграл справа определён, так как там $t$ бегает в $\bar G$. Но я пока дальше не соображу, что сделать.