Решил освоить геометрию по трехтомнику Понарина.
И уже в первом параграфе испытал некоторый затык.
Параграф посвящен углам, ассоциированным с окружностями.
К параграфу прилагается 8 задач.
Я решил пока только четыре: 1,2,3,8.
Но опубликую их все. Мне кажется, они не самого примитивного уровня.
И могут быть полезными для углубленного изучения геометрии.
Предлагается не выкладывая полных решений публиковать конструктивные идеи.
Задачи1.1. Не пользуясь формулами площади треугольника, докажите, что высота треугольника равна произведению не соответственных ей сторон, деленному на диаметр описанной около
этого треугольника окружности.
1.2. Две окружности касаются внешне в точке

. Общая внешняя касательная к этим окружностям касается их в точках

и

. Докажите, что угол

прямой.
1.3. Две окружности касаются внутренним образом в точке

. Хорда

большей окружности касается меньшей окружности в точке

. Докажите, что луч

делит угол

пополам.
1.4. В треугольник

вписана окружность, касающаяся сторон

и

в точках

и

. Докажите, что центр окружности, вписанной в треугольник

, принадлежит первой окружности.
1.5. В окружность вписан четырехугольник

. Точки

,

,

,

являются соответственно серединами дуг

,

,

,

. Докажите, что прямые

и

перпендикулярны.
1.6. Около треугольника

описана окружность. Биссектрисы его углов

,

,

пересекают эту окружность соответственно в точках

,

,

. Докажите, что прямые

,

,

перпендикулярны сторонам треугольника

.
1.7. Прямые

,

,

, содержащие высоты остроугольного треугольника

, пересекают описанную около него окружность в точках

,

,

. Докажите, что эти прямые содержат биссектрисы углов треугольника

.
1.8. Биссектрисы углов

и

треугольника

пересекаются в точке

. Биссектриса угла

вторично пересекает описанную около треугольника

окружность в точке

. Докажите, что
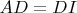
.
Переносы убрал. Смысл публикации простой. Изучаю геометрию. Прошу помощи разобраться.
Если у кого есть ссылка на решебник в сети, буду признателен. Очевидно что я не учащийся и не халявщик. Просто последнее время геометрия покоя не дает. Ну и потом ищу соратников по этому благому делу. Мне кажется подобрал подходящий учебник-задачник. Поначалу публиковал задачи повышенной сложности в олимпиадном отделе. Но мне они там пока не по зубам. Хотя ответы есть на руках. Задумка же простая - за короткое время прорешать все задачки из этого пособия, может быть в составе коллектива энтузиастов.
Может имеет смысл сразу перенести тему в раздел Геометрия, чтобы здесь не мозолила глаза.