Мне как раз не ясно, как воспользоваться этим свойством сравнений из-за большой степени.
Потому что она - большая и страшная?

Давайте ее тоже заменим на букву

, чтобы она не была такая страшная

Надо вычислить

.
Вот теперь попробуйте:
1. Выделить степень

отдельно, остальное (которое взаимно простое) - отдельно.
2. Вынести НОД за скобку. (считайте, что

)
3. Упростить то, что осталось от степени

.
Получается?
Просто если я и применял это свойство, то для чисел вроде

, для которых всё было довольно просто:

.
Да и тут точно так же надо действовать.
Вообще интересно, возможна ли и насколько полезна будет общая формула, которая работала бы в любом случае, без выделения случая НОД?

upd: кажется так:
Если

для любых


Формула корректна, поскольку

- единственное значение по модулю

. Кроме того
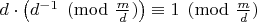
.
Обобщать формулу с функцией Кармайкла лень

upd2: хотя я же забыл: там м.б. сколь угодно длинный предпериод, так что красивой формулы действительно не получится, только если добавлять какие-то частые и удобные условия. Например,

.
Например, если

, то

. А это уже очень удобно для символьных преобразований

(равносильное условие
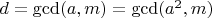
).
При этих условиях

.
Вот можете это юзать
