1).Define a relation

on the set

of real numbers, by setting

.
2).Prove that this is an equivalence relation, and find a 'compelling' description for

.
3).Do the same for the relation

on the plane

defined by declaring
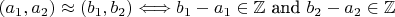
.
1). Что имеется ввиду "определить отношение"? Оно разве не определено собственно тем, что задано:

?
2). ...find a 'compelling' description for

. Не понятно как записать

? Понятно, что это будут классы эквивалетности для всех действительных чисел на
![$[0, 1]$ $[0, 1]$](https://dxdy-03.korotkov.co.uk/f/e/8/8/e88c070a4a52572ef1d5792a341c090082.png)
.
Если что, то

это множетство классов эквивалентности элементов

относительно отношения

.
Например, для
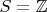
и

четное. Тогда
![$\mathbb {Z}/ \sim = \{[0]_{\sim}, [1]_{\sim}\}$ $\mathbb {Z}/ \sim = \{[0]_{\sim}, [1]_{\sim}\}$](https://dxdy-02.korotkov.co.uk/f/d/b/8/db84da33bad40c91dfcbca5ae2cca40582.png)