Не должен. Можно для любого

утверждать, что поворот на

тоже является образующим, а при

он отличен от поворота на

. Есть и много других образующих.
Понял, не подумал об этом.
Постройте центр квадрата и соедините его отрезками со всеми вершинами квадрата. Какой минимальный угол между этими отрезками?
Аналогично и в общем случае: постройте центр правильного

-угольника

и соедините его отрезками со всеми его вершинами. Какой минимальный угол между этими отрезками?
Возьмём центр правильного

-угольника, соединим его отрезками со всеми вершинами нашего многоугольника. Минимальный угол между отрезками получается как раз -

, так как мы разбили имеющиеся 360 градусов

отрезками.
Если взять угол, меньший, чем этот, мы увидим, что при повороте на него не произойдет самосовмещения. Если взять больший - тоже. Значит можно считать поворот на такой угол относительно центр правильного многоугольника движением.
Далее мы видим, что у нас есть нулевой элемент, есть обратный, ясно, что есть ассоциативность. Нам осталось лишь доказать, что поворот является бинарной операцией, то есть группа замкнута. И так как мы уже установили, что
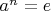
, получим циклическую группу.
Верная ли мысль?
Вообще да, нам действительно еще придется взять группу движений 1-го рода

и доказать, что там есть лишь повороты относительно центра на угол, кратный

. Это несложно тоже, но еще зависит от того, какими геометрическими утверждениями Вы можете пользоваться. Например, знаете ли Вы, что все движения 1-го рода - это только переносы и повороты? Если да, то можно просто заметить, что переносы не подходят, затем проверить, куда переходит при поворотах центр

. Куда переходят его вершины? Какое отсюда следует свойство угла поворота?
Если Вы не знаете про движения 1-го рода, то тогда Вам будет сложнее. Но вообще не хотелось бы усложнять простую учебную задачу на теорию групп решением более сложной задачи о структуре группы движений на плоскости

Тогда просто считайте, что Вам дано множество

поворотов

относительно его центра и доказывайте утверждения для него.
Нет, пока не знаю про движения плоскости. Помимо этой книги я также смотрю лекции Савватеева ("Теория групп в геометрии"), но там пока что остановился на движениях окружности.
Кстати, можно не использовать явный вид элементов этой группы. Можно рассмотреть абстрактно

как множество преобразований, переводящих

в себя. И только отсюда сразу вывести, что

- замкнуто относительно композиции. Можете выбрать любой удобный Вам способ.
Попробую доказать пока без абстракций.
Пусть

- поворот на

градусов, а

- на

. Рассмотрим композицию этих поворотов :

. Ясно, что если последовательно применить преобразование

, а затем

, то это будет поворот на

. Если обозвать

как

, то мы получили поворот на

градусов. Ясно, что мы "не вывалились" за наши движения, так как мы

раз повернули наш многоугольник на угол в

градусов, а мы доказали, что этот поворот - движение.
Имеем совокупность поворотов, для которых выполнены все аксиомы группs, для которой мы, вдобавок, нашли образующий элемент. Мы видим, что все элементы этой группы - просто композиции нашего образующего самим с собой. В группе поворотов нет более элементов, кроме
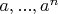
, значит наша группа - циклическая группа порядка n.
Укажите, пожалуйста, на недочеты и ошибки.