Минимизация функционала на дискретном множестве

[m09kaa4]

Здравствуйте.

Пусть $t_1, \dots, t_n$, $n > 4$ -- некоторые фиксированные моменты времени; $R(t)$ -- матрица поворота в трехмерном пространстве вокргу оси $z$; $e_{k}, k \in [1 : N], r_1, r_2$ -- заданные точки на сфере.
Рассмотрим следующие матрицы: $C(k_1, \dots, k_n) = \left \{ e_{k_i}^T \frac{d}{dt}R(t_i) (r_2 - r_1), \left (e_{k_i}^T R(t_i) r_1 \right )^{-1}, \left (e^T R(t_i) r_2 \right )^{-1}, 1 \right \}_{i=1}^{n}$, $A(k_1, \dots, k_n) = \left (C^TC \right )^{-1}$. Требуется найти такой набор индексов $ (k_1, \dots, k_n) \in [1 : N]^n$, что сумма диагональных элементов матрицы $A$ минимальна и выполнено условие: для любых $k_i$ значения $e_{k_i}^T R(t_i) r_1$, $e^T R(t_i) r_2$ больше нуля:

$ \underset{ \begin{matrix} (k_1, \dots, k_n) \in [1 : N]^n\\ \forall k_i: e_{k_i}^T R(t_i) r_1 > 0,\\ \qquad e_{k_i}^T R(t_i) r_2 > 0 \end{matrix} }{argmin }\left (\sum_{i = 1}^{n}A_{i,i}(k_1, \dots, k_n) \right ) $.


Эта задача появилась из некоторых физических соображений, и на самом деле искать минимум не нужно. Скорее нужно найти некоторый алгоритм, который бы давал решение сильно лучше, чем получалось бы при случайном выборе набора индексов (для проверки будет сделана какая-нибудь симуляция).

Число точек $N$ множества $ \left \{ e_k \right \} $ и число строк $n$ матрицы $C$ достаточно большие, так что тупым перебором не получится найти хорошее решение. С другой стороны, это число не достаточное, чтобы рассмотреть функцию $(S^2)^n \rightarrow \mathbb{R}$, численно найти некоторую совокупность "маленьких" локальных минимумов, а потом в множестве $\left \{ e_k \right \}$ искать наиболее "похожую" последовательность точек (хотя именно это я сейчас пытаюсь сделать). А других мыслей у меня нет.

Если у вас есть какие-то идеи насчет того, как можно решить данную задачу, либо вы знаете литературу, в которой что-то подобное описано, пожалуйста, посоветуйте мне.

Заранее спасибо.

[svv]

m09kaa4 в сообщении #1271875 писал(а):

$\underset{...}{\operatorname{argmin}}\left (\sum_{i = 1}^{n}A_{i,i}(k_1, \dots, k_n) \right )$

Мне кажется, сумма тут должна быть от $1$ до $4$.

[m09kaa4]

svv в сообщении #1272096 писал(а):

m09kaa4 в сообщении #1271875 писал(а):

$\underset{...}{\operatorname{argmin}}\left (\sum_{i = 1}^{n}A_{i,i}(k_1, \dots, k_n) \right )$

Мне кажется, сумма тут должна быть от $1$ до $4$.

Да, конечно. Был невнимателен.

[svv]

m09kaa4 в сообщении #1271875 писал(а):

Скорее нужно найти некоторый алгоритм, который бы давал решение сильно лучше, чем получалось бы при случайном выборе набора индексов

Скажите, а не может ли оказаться, что хорошие результаты получаются именно при случайном выборе точки $e_k$ для каждого момента времени?

Вот какие мысли у меня были.

Собственные значения $\lambda_i$ матрицы $C^TC$, в силу её структуры, неотрицательны. Чтобы $C^TC$ была обратимой, среди $\lambda_i$ не должно быть и нулевого. Тогда все $\lambda_i>0$.
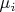
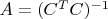
Собственные значения $\mu_i$ матрицы $A=(C^TC)^{-1}$ равны $\mu_i=(\lambda_i)^{-1}$, и аналогично все $\mu_i>0$.

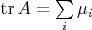
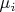
Мы хотим, чтобы след матрицы $A$ был малым. Так как $\operatorname{tr}A=\sum\limits_i \mu_i$, то должно быть малым максимальное из $\mu_i$. То есть должно быть большим минимальное из $\lambda_i$.

Этого, однако, не будет, если столбцы матрицы $C$ будут почти линейно зависимы, то есть если прибавлением к одному из столбцов $C$ (с номером $j$) линейной комбинации остальных столбцов мы можем сделать все элементы $j$-го столбца очень малыми числами. Тогда у $C^TC$ одно из собственных значений $\lambda_i$ будет очень малым, что, как мы выяснили выше, плохо.

Теперь представим, что точек $e_k$ очень-очень много и они примерно равномерно распределены по сфере (я буду считать, что она единичного радиуса). Попробуем несколько «детерминированных» стратегий выбора точки для каждого момента времени $t_i$. Можно, например, выбирать $e_k$, ближайшую к $R(t_i)r_1$. Но тогда числа, стоящие во втором столбце $C$, будут близки к $1$. Отняв от второго столбца четвёртый, получим во втором очень малые числа.

Можно, наоборот, подбирать $e_k$ так, чтобы векторы $e_k$ и $R(t_i)r_1$ были почти ортогональны. Тоже ничего хорошего: во втором столбце сразу будут почти нули. И вообще, стремление к тому, чтобы скалярные произведения $(e_{k_i},R(t_i)r_1)$ и/или $(e_{k_i},R(t_i)r_2)$ были заданными константами для всех $i$, делает столбцы $C$ почти линейно зависимыми.

Ну хорошо, а давайте для части $t_i$ выбирать точку $e_k$, ближайшую к $R(t_i)r_1$, а для другой части — ближайшую к $R(t_i)r_2$. Результат тот же.

Тут я и подумал, что, возможно, случайный выбор точки $e_k$ будет давать результат, близкий к оптимальному.

[DeBill]

m09kaa4 в сообщении #1271875 писал(а):

; $R(t)$ -- матрица поворота в трехмерном пространстве вокргу оси $z$;

На угол $t$? Или это некая заданная функция от $t$?

[m09kaa4]

DeBill,на угол t.

svv, Не совсем Вас понял.
Вы утверждаете, что распределение всевозможных результатов имеет маленькую дисперсию, и потому брать случайную последовательность хорошая стратегия?
Думаю, стратегии все-такие есть. И в случае непрерывной задачи (то есть когда нет фиксированных $e_i$ и можно выбирать любую точку сферы) оптимальный выбор сильно лучше случайного. Точек $e_i$ около двухсот, возможно, если найти много "хороших" последовательностей, на которых функция имеет малое значение, при равномерном распределении $e_i$ "хороших" последовательностей будут находиться последовательности $e_{k_1}, \dots, e_{k_n}$.
Я сделаю симуляцию и попытаюсь построить какие-то гистограммы.

[svv]

Строгих рассуждений, которые бы показывали это, у меня нет. Меня просто смутило то, что несколько навскидку взятых стратегий все оказались «хорошим способом получить гарантированно плохой результат».

[m09kaa4]

Возникла одна идея, позволяющая построить жадный алгоритм.
Пусть, как в первом посте, $A(k_1, \dots, k_N) = \left (C^TC \right )^{-1}$.
В каждый момент времени нам доступен лишь небольшое подмножество сферы, пусть это подмножество содержит точки $\{e_{N_1}, \dots, e_{N_l}\}$. Каждой такой точке соответствует строчка $C_{N_i}$.

Тогда, применяя формулу Шермана, имеем:

$ A(k_1, \dots, k_{N+1}) = A_{N+1} = \left( A^{-1}_N + C_{(N+1)_i}^T C_{(N+1)_i} \right)^{-1} = A_{N} - \frac{A^{T}_NC^T_{(N+1)_i}C_{(N+1)_i}A_N}{1 + C_{(N+1)_i} A_N C_{(N+1)_i}^T}$.

Отсюда видно, что, если мы знаем хорошую последовательность для моментов времени $t_1, \dots, t_N$ и соответствующую ей матрицу $A_N$, то можем найти лучшую из возможных ее продолжений. Правда, из-за жадности глобальный минимум мы не обязаны получить. Но это можно слегка поправить, например, не ища каждый раз лучшее продолжение, а обрубая худшие.