У меня есть программа, которая находит вид функции по экспериментальным данным. Не исключено, что с помощью нее можно найти подходящую функцию и для этой задачи.
Судя по картинке, нужно найти функцию от одного аргумента x, т.е. функцию

. Очевидно, что эта функция зависит от параметров углов и радиусов.
Первый же вопрос - сколько функций нужно найти, одну или две? На картинке две кривые - должна ли задача решаться задача поиска двух функций? Или это задача поиска одной функции, для которой обе кривые совпадут при нулевых радиусах?
Второй вопрос - это задание ограничений для искомой функции (функций). Как уже отметил
svv, ограничения для функции проще задавать в виде координат и производных. Если все же нужно искать одну функцию, то параметров всего 4:
* Производная в 0
* Производная в 1 (b можно положить равным 1)
* Точка
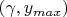
Ну, и далее следует задать ограничения на функцию:
* Функция строго вогнутая
* Производная в

равна нулю
* Для гладкости можно задать что-то вроде этого

Если это так, то можно попытаться найти подходящую функцию - нужно будет только сгенерировать данные с разными значениями параметров.