Здравствуйте!
Решил несколько задач на функциональные ряды, но хотелось бы удостовериться, что делаю все правильно.
Проверьте, пожалуйста, решения:
(1) Найти область сходимости функционального ряда:
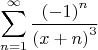
Решение: Т.к. знаменатель не должен равняться нулю

, то

. Другими словами, исключаем все целые отрицательные значения

.
Далее, потому как ряд не является знако-положительным, рассмотрим ряд состоящий из модулей членов исходного ряда:

И сравним данный ряд с рядом

, сходящимся как ряд Дирихле. Предел отношения этого ряда и ряда модулей при

равен единице, а значит по предельному признаку сравнения ряд модулей сходится вместе с ним, а значит исходный ряд сходится абсолютно на всей числовой прямой, за исключением целых отрицательных значений

.
(2) Найти сумму ряда:

Раскрываю скобки и разбиваю получившийся ряд на сумму двух:

Обозначим за

сумму ряда

, а за

сумму ряда

. Тогда

будет суммой исходного ряда.
1)

при

2) По членно продифференцируем ряд

и вынесем за знак суммы

, тогда при

ряд производных будет сходиться к
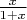
. Теперь проинтегрируем получившуюся функцию по

от

до

. В результате получим, что

(при

)
В таком случае, сумма исходного ряда:

(3) Для ряда

построить мажорирующий ряд и доказать равномерную сходимость на отрезке
![$[-3; 3]$ $[-3; 3]$](https://dxdy-02.korotkov.co.uk/f/9/e/d/9ed3bda645d05c3691bc50d6f8e93f3c82.png)
Рассмотрим числовой ряд

По радикальному признаку Коши он сходится:

.
И т.к.

, это значит исходный ряд мажорируется сходящимся числовым рядом, а значит по признаку Вейерштрасса исходный ряд сходится равномерно.
Помогите, пожалуйста, выявить неточности и ошибки в решении и устранить их.