Необходимо построить векторное поле без особых точек на нечетномерной сфере.
Решение у меня такое. Сфера находится в четномерном пространстве, поэтому каждой точке сферы

можно сопоставить вектор

. То есть задать перпендикулярный вектор. Это, вроде, понятно. Но возникает необходимость доказать, что касательный вектор в данной точке сферы перпендикулярен радиус-вектору.
Нашел вот какое решение данного вопроса.
Гладкой кривой

на сфере соответствует вектор

, для которого выполняется равенство

. Действительно, из равенства
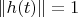
следует, что

, поэтому

.
И вот здесь вопросы. Правильно ли я понимаю, что рассматриваю касательный вектор как класс эквивалентных кривых? Беру кривую, раскладываю в ряд Тейлора, дифференцирую при нулевом

и получаю

как касательный вектор?
А дальше совсем непонятно. Что за норма кривой и почему она равна 1?