Задача поставлена так:

Предлагаю такое решение:
Решаем вспомогательную задачу

при нулевых условиях

,

и дополнительных

. Решение задачи обозначим

, но до выписывания решения будем искомую функцию обозначать

.
(Спойлер)
Исходя из граничных условий пишем

откуда

Уравнение Лапласа в указанном разложении имеет вид

где

. Решение последнего уравнения

(наличие только

обусловлено условием

, которое очевидно получается из

). Коэффициент

получается из условия
![$$\begin{align*}
\varphi_{kl}(c)
&= \dfrac{4}{ab} \int \limits_0^a \int \limits_0^b \sin \dfrac{\pi k x}{a} \sin \dfrac{\pi l y}{b} \psi_{(z)}(x, y) \, \mathrm d x \, \mathrm d y
= \dfrac{4}{ab} \int \limits_0^a \int \limits_0^b \sin \dfrac{\pi k x}{a} \sin \dfrac{\pi l y}{b} x^2 y c \, \mathrm d x \, \mathrm d y = \\
&= \dfrac{4c}{ab} \int \limits_0^a x^2 \sin \dfrac{\pi k x}{a} \, \mathrm d x \int \limits_0^b y \sin \dfrac{\pi l y}{b} \, \mathrm d y
= \dfrac{4c}{ab} \cdot \dfrac{a^3}{\pi^3 k^3} \cdot \dfrac{b^2}{\pi^2 l^2} \int \limits_0^a \dfrac{\pi^2 k^2 x^2}{a^2} \sin \dfrac{\pi k x}{a} \, \mathrm d \left( \dfrac{\pi k x}{a} \right) \times \\
&\times \int \limits_0^b \dfrac{\pi l y}{b} \sin \dfrac{\pi l y}{b} \, \mathrm d \left(\dfrac{\pi l y}{b}\right)
= \dfrac{4 a^2 b c}{\pi^5 k^3 l^2} \int \limits_0^{\pi k} t^2 \sin t \, \mathrm d t \int \limits_0^{\pi l} t \sin t \, \mathrm d t = \\
&= \dfrac{4 a^2 b c}{\pi^5 k^3 l^2} \left[ (2 - \pi^2 k^2) (-1)^k - 2 \right] \cdot \left[ - \pi l (-1)^l\right]
= \dfrac{4 a^2 b c}{\pi^4 k^3 l} \left[ 2(1 - (-1)^k) + \pi^2 k^2 \right] (-1)^l = \\
&= \dfrac{8 a^2 b c [1 - (-1)^k](-1)^l}{\pi^4 k^3 l} + \dfrac{4 a^2 b c (-1)^l}{\pi^2 k l}, \qquad A_{kl}
= \dfrac{\varphi_{kl}(c)}{\sh (R_{kl} c)}.
\end{align*}$$ $$\begin{align*}
\varphi_{kl}(c)
&= \dfrac{4}{ab} \int \limits_0^a \int \limits_0^b \sin \dfrac{\pi k x}{a} \sin \dfrac{\pi l y}{b} \psi_{(z)}(x, y) \, \mathrm d x \, \mathrm d y
= \dfrac{4}{ab} \int \limits_0^a \int \limits_0^b \sin \dfrac{\pi k x}{a} \sin \dfrac{\pi l y}{b} x^2 y c \, \mathrm d x \, \mathrm d y = \\
&= \dfrac{4c}{ab} \int \limits_0^a x^2 \sin \dfrac{\pi k x}{a} \, \mathrm d x \int \limits_0^b y \sin \dfrac{\pi l y}{b} \, \mathrm d y
= \dfrac{4c}{ab} \cdot \dfrac{a^3}{\pi^3 k^3} \cdot \dfrac{b^2}{\pi^2 l^2} \int \limits_0^a \dfrac{\pi^2 k^2 x^2}{a^2} \sin \dfrac{\pi k x}{a} \, \mathrm d \left( \dfrac{\pi k x}{a} \right) \times \\
&\times \int \limits_0^b \dfrac{\pi l y}{b} \sin \dfrac{\pi l y}{b} \, \mathrm d \left(\dfrac{\pi l y}{b}\right)
= \dfrac{4 a^2 b c}{\pi^5 k^3 l^2} \int \limits_0^{\pi k} t^2 \sin t \, \mathrm d t \int \limits_0^{\pi l} t \sin t \, \mathrm d t = \\
&= \dfrac{4 a^2 b c}{\pi^5 k^3 l^2} \left[ (2 - \pi^2 k^2) (-1)^k - 2 \right] \cdot \left[ - \pi l (-1)^l\right]
= \dfrac{4 a^2 b c}{\pi^4 k^3 l} \left[ 2(1 - (-1)^k) + \pi^2 k^2 \right] (-1)^l = \\
&= \dfrac{8 a^2 b c [1 - (-1)^k](-1)^l}{\pi^4 k^3 l} + \dfrac{4 a^2 b c (-1)^l}{\pi^2 k l}, \qquad A_{kl}
= \dfrac{\varphi_{kl}(c)}{\sh (R_{kl} c)}.
\end{align*}$$](https://dxdy-02.korotkov.co.uk/f/5/c/6/5c67fc442f144f2b0b4f273e3d208aba82.png)
Итак, решение вспомогательной задачи даётся выражением
![$$
\varphi_{1} = \dfrac{4 a^2 b c}{\pi^2} \sum \limits_{k = 0}^\infty \sum \limits_{l = 0}^\infty \dfrac{(-1)^l}{k l} \left[\dfrac{2 [1 - (-1)^k]}{\pi^2 k^2} (-1)^l + 1\right] \dfrac{\sh(R_{kl} z) }{\sh (R_{kl} c)} \sin \dfrac{\pi k x}{a} \sin \dfrac{\pi l y}{b}.
$$ $$
\varphi_{1} = \dfrac{4 a^2 b c}{\pi^2} \sum \limits_{k = 0}^\infty \sum \limits_{l = 0}^\infty \dfrac{(-1)^l}{k l} \left[\dfrac{2 [1 - (-1)^k]}{\pi^2 k^2} (-1)^l + 1\right] \dfrac{\sh(R_{kl} z) }{\sh (R_{kl} c)} \sin \dfrac{\pi k x}{a} \sin \dfrac{\pi l y}{b}.
$$](https://dxdy-01.korotkov.co.uk/f/0/2/2/022a8f4c5c61311f20c1547e3a85060682.png)
Теперь будем решать вспомогательную задачу

при нулевых условиях

,

и дополнительных

. Решение задачи обозначим

, но до выписывания решения будем искомую функцию обозначать

.
(Спойлер)
Исходя из граничных условий построим разложение

откуда

Уравнение Лапласа в указанном разложении имеет вид

где
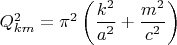
. Решение последнего уравнения

(наличие только

обусловлено условием

, которое очевидно получается из

). Коэффициент

получается из условия
^m}{\pi^4 k^3 m} + \dfrac{4 a^2 b c (-1)^m}{\pi^2 k m}, \\ B_{km}
= \dfrac{\varphi_{km}(b)}{\sh (Q_{km} b)}.
\end{align*}
$$ $$\begin{align*}
\varphi_{km}(b)
&= \dfrac{4}{ac} \int \limits_0^a \int \limits_0^c \sin \dfrac{\pi k x}{a} \sin \dfrac{\pi m z}{c} \psi_{(y)}(x, z) \, \mathrm d x \, \mathrm d z
= \dfrac{4}{ac} \int \limits_0^a \int \limits_0^c \sin \dfrac{\pi k x}{a} \sin \dfrac{\pi m z}{c} x^2 b z \, \mathrm d x \, \mathrm d z = \\
&=\ldots = \dfrac{4 a^2 b c}{\pi^5 k^3 m^2} \int \limits_0^{\pi k} t^2 \sin t \, \mathrm d t \int \limits_0^{\pi m} t \sin t \, \mathrm d t = \dfrac{8 a^2 b c [1 - (-1)^k](-1)^m}{\pi^4 k^3 m} + \dfrac{4 a^2 b c (-1)^m}{\pi^2 k m}, \\ B_{km}
= \dfrac{\varphi_{km}(b)}{\sh (Q_{km} b)}.
\end{align*}
$$](https://dxdy-02.korotkov.co.uk/f/5/c/e/5ceb536f35d6686568f4dcd0c2f38e6782.png)
Итак, решение вспомогательной задачи даётся выражением
![$$
\varphi_{2} = \dfrac{4 a^2 b c}{\pi^2} \sum \limits_{k = 0}^\infty \sum \limits_{m = 0}^\infty \dfrac{(-1)^m}{k m} \left[\dfrac{2 [1 - (-1)^k]}{\pi^2 k^2} (-1)^m + 1\right] \dfrac{\sh(Q_{km} y) }{\sh (Q_{km} b)} \sin \dfrac{\pi k x}{a} \sin \dfrac{\pi m z}{c}.
$$ $$
\varphi_{2} = \dfrac{4 a^2 b c}{\pi^2} \sum \limits_{k = 0}^\infty \sum \limits_{m = 0}^\infty \dfrac{(-1)^m}{k m} \left[\dfrac{2 [1 - (-1)^k]}{\pi^2 k^2} (-1)^m + 1\right] \dfrac{\sh(Q_{km} y) }{\sh (Q_{km} b)} \sin \dfrac{\pi k x}{a} \sin \dfrac{\pi m z}{c}.
$$](https://dxdy-03.korotkov.co.uk/f/a/f/b/afbe6aea3342863964925d3b57eaef0082.png)
Решаем вспомогательную задачу

при нулевых условиях

,

и дополнительных

. Решение задачи обозначим

, но до выписывания решения будем искомую функцию обозначать

.
(Спойлер)
Исходя из граничных условий пишем

откуда

Уравнение Лапласа в указанном разложении имеет вид

где

. Решение последнего уравнения

(наличие только

обусловлено условием

, которое очевидно получается из

). Коэффициент

получается из условия

Итак, решение вспомогательной задачи даётся выражением

Решение исходной задачи, ясно, есть

. Чтобы уважаемые участники не лазили под спойлеры в поисках смысла обозначений, продублирую их:

Прошу проверить хотя бы приведённый ответ. Я не знаю, как это можно сделать независимым способом, но поскольку я чрезвычайно часто ошибаюсь, хотел бы спросить: а я вообще всё правильно понял, как решать такие задачи? (Нам сказали, что это называется методом разделения переменных, но показали только для двумерного случая).
Спасибо, если продерётесь.
P. S. Допустим, что ответ в такой форме верен. Как исследовать сходимость этих рядов?