Некомпактность и неполнота

[Mikhail_K]

Заинтересовал вопрос.

Верно ли, что любое некомпактное метрическое пространство гомеоморфно некоторому неполному метрическому пространству?

Обратное утверждение очевидно (если метрическое пространство гомеоморфно неполному, то оно некомпактно, потому что компактность сохраняется при гомеоморфизме и все компактные пространства полные). Так что, если и прямое верно, то получилось бы красиво: что компактность - это такой топологический аналог полноты, что компактность - это существенная полнота, неустранимая при гомеоморфизмах.

Для подпространств $\mathbb{R}^n$ (и, в частности, для некомпактных многообразий) утверждение верно: если некомпактное множество незамкнуто в $\mathbb{R}^n$, то оно и так неполно, а если неограничено, то переводится в незамкнутое гомеоморфизмом, отображающим $\mathbb{R}^n$ на открытый шар. Если взять в качестве некомпактного пространства счётное пространство изолированных точек, то оно гомеоморфно неполному $\{1/n\,|\,n\in\mathbb{N}\}$; такой же фокус получится и с несчётным.

А можно ли это доказать (или опровергнуть) в общем случае?

[Brukvalub]

Mikhail_K в сообщении #1262387 писал(а):

Для подпространств $\mathbb{R}^n$ утверждение верно: если компактное множество незамкнуто в $\mathbb{R}^n$, то оно и так неполно,

Вы можете привести пример такого множества?

[Mikhail_K]

Brukvalub в сообщении #1262395 писал(а):

Вы можете привести пример такого множества?

Это была опечатка (к сожалению, не единственная), я её уже исправил.

[DeBill]

Mikhail_K
Мы умеем непрерывно отображать полное некомпактное $\mathbb{R}$ на неполное "интервал". Аеалогично: плоскость - на открытый круг.
Возбудившись этими примерами, можно попробовать такую конструкцию:
Выберем в некомпактном метрическом последовательность $\{ a_n \}$, с попарными расстояниями большими $\varepsilon$ (равному, для простоты, 2). Испортим метрику: в шаре $B_1(a_n)$, старое расстояние умножим на $\frac{1}{2^n}$. Расстояние между точками из $B_1(a_n)$ и $B_1(a_m) $ положим равным $\frac{1}{2^n}- \frac{1}{2^m}$, прочие расстояния определим так, чтоб неравенство тр-ка было (как? Типа, так: возьмем первые 100 шаров, и в объединении их 50-окрестностей, расстояние определим как инфинум длин ломаных , соединяющих точки, в предыдущей метрике. Вроде, при увеличении 100 и 50, все устаканится???).
Вот. Тогда тождественное будет искомым гомеоморфизмом...

[Mikhail_K]

Итак, попробую описать это подробнее.

Компактные метрические пространства - это полные и вполне ограниченные. Вот у нас есть некомпактное пространство. Если оно неполное, то больше ничего не нужно. Пусть оно полное, но не вполне ограниченное, то есть для некоторого $\varepsilon>0$ у него нет конечной $\varepsilon$-сети. Возьмём в этом пространстве произвольно точку $a_1$ и начнём с неё строить последовательность, каждый раз выбирая новую точку $a_n$ на расстоянии больше чем $\varepsilon$ от всех предыдущих точек $a_1,\ldots,a_{n-1}$. Если на каком-то этапе этого не получилось сделать, то $\{a_1,\ldots,a_{n-1}\}$ есть конечная $\varepsilon$-сеть и противоречие. Значит, последовательность $\{a_n\}$ с попарными расстояниями больше $\varepsilon$ у нас построится.

А то, вообще-то не в любых некомпактных пространствах есть такие последовательности. В интервале нету например.

Сейчас попробую осмыслить вторую, ключевую часть.

[Mikhail_K]

DeBill в сообщении #1262413 писал(а):

старое расстояние умножим на $\frac{1}{2^n}$

Кажется, на $1/2^{n+1}$ надо? Расстояния внутри шара не превышают $2$, а сумма расстояний от двух точек $n$-го шара до какой-то точки $m$-го не меньше чем $1/2^{n+1}+1/2^{n+1}=1/2^n$.

DeBill в сообщении #1262413 писал(а):

как? Типа, так: возьмем первые 100 шаров, и в объединении их 50-окрестностей, расстояние определим как инфинум длин ломаных , соединяющих точки, в предыдущей метрике. Вроде, при увеличении 100 и 50, все устаканится???

Боюсь, что не улавливаю Вашу идею. Каких ломаных? В какой метрике? Почему нельзя взять сразу все шары?

[Mikhail_K]

----------
Итак, построена $\{a_n\}$ такая, что попарные расстояния между членами последовательности больше $\varepsilon$.
Рассмотрим замкнутые шары $B_{\varepsilon/4}(a_n)$ (т.е. в обозначениях DeBill радиусы шаров должны быть $1/2$, а не $1$).

Пусть $\rho(x,y)$ - первоначальная метрика. Будем строить новую метрику в несколько этапов.
Вначале построим "недо-метрику" (не являющуюся метрикой) следующим образом:
$\rho^*(x,y)=2^{-n}\rho(x,y)$, если $x,y\in B_{\varepsilon/4}(a_n)$ (максимальное расстояние здесь будет $2^{-n-1}\varepsilon$);
$\rho^*(x,y)=|2^{-n-1}-2^{-m-1}|\varepsilon$, если $x\in B_{\varepsilon/4}(a_n)$, $y\in B_{\varepsilon/4}(a_m)$, $n\neq m$ (в рамках шаров аксиомы метрики выполнены);
$\rho^*(x,y)=\rho(x,y)$ во всех других случаях (здесь уже аксиомы метрики могут нарушиться).

На втором этапе строим окончательную метрику $\rho^{**}(x,y)$ как инфимум всевозможных конечных длин ломаных, соединяющих $x$ и $y$, в "недо-метрике" $\rho^*(x,y)$.

Вроде бы получается:
$\rho^{**}(x,y)=\rho^*(x,y)$ если обе точки $x,y$ принадлежат шарам;
$\rho^{**}$ удовлетворяет всем аксиомам метрики;
$\rho^{**}(x_n,x_0)\to 0$ тогда и только тогда, когда $\rho(x_n,x_0)\to 0$, так что пространство с $\rho^{**}$ гомеоморфно исходному;
последовательность $\{a_n\}$ фундаментальна в пространстве с метрикой $\rho^{**}$, но не сходится, так что оно неполное.

Не могу найти ошибку (хотя и не могу избавиться от сомнений, что что-то не так).

[Someone]

Идея использовать бесконечное дискретное множество правильная. Осталось только придумать метрику, которая была бы эквивалентна исходной (полной), и для которой это множество содержало бы фундаментальную последовательность (эта последовательность, естественно, никуда сходиться не будет). Я как-то не вижу никакого простого способа модифицировать заданную полную метрику так, чтобы этого добиться.

Но можно попытаться построить требуемую метрику, модифицировав конструкцию, используемую в доказательстве метризационной теоремы Бинга—Нагаты—Смирнова.

П. С. Александров, Б. А. Пасынков. Введение в теорию размерности. Введение в теорию топологических пространств и общую теорию размерности. "Наука", Москва, 1973.
Глава 1, § 11, теорема 16.

Р. Энгелькинг. Общая топология. Москва, "Мир", 1986.
Теорема 4.4.7.

Mikhail_K, извините, сразу понять, правильное ли у Вас доказательство, не смог. Особенно вызывает сомнения то, что происходит на границе шаров. Возможно, всё будет благополучно.

[vpb]

Предлагаю другую конструкцию, там наверное проще будет доказать, что всё нормально. Пусть $\{a_i\}$ --- последовательность такая, что попарные расстояния между $a_i$ все $\geq1$. А $X$ --- наше пространство. Добавим к нему еще одну точку: $X'=X\cup\{p\}$. Для некоторых пар из $X'$ определим число $\sigma(x,y)$, а именно $\sigma(x,y)=\rho(x,y)$ при $x,y\in X$, $\sigma(p,a_i)=\sigma(a_i,p)= 2^{-i}$, в остальных случаях $\sigma(x,y)$ не определено. Теперь для $x,y\in X'$ пусть $\tau(x,y)$ --- инфимум $\sigma$-длин ломаных, в которых для каждых двух соседних вершин $\sigma$ определено, a $\rho'$ --- ограничение $\tau$ на $X$. Что $\rho'$ всюду определено на $X$, симметрично и удовлетворяет треугольнику --- ясно. Допустим, $\rho'(x,y)=0$, но $x\ne y$. Тогда для каждого $\varepsilon>0$ существует ломаная в $X'$ из $x$ в $y$, $\sigma$-длины $<\varepsilon$. Целиком внутри $X$ она лежать не может, иначе ее длина $\geq\rho(x,y)$. Значит проходит через $a_i$, причем $\rho(x,a_i)<\varepsilon$. Получаем, что для каждого $\varepsilon$ существует $i$ такое, что $\rho(x,a_i)<\varepsilon$. Это возможно, только если $x$ --- одно из $a_i$. Аналогично для $y$. ... ну, конец доказательства думаю ясен.

[pogulyat_vyshel]

DeBill в сообщении #1262413 писал(а):

Мы умеем непрерывно отображать полное некомпактное $\mathbb{R}$ на неполное "интервал". Аеалогично: плоскость - на открытый круг.
Возбудившись этими примерами, можно попробовать такую конструкцию:

я вот возбудился и вспомнил, что всякое метрическое пространство изометрично изоморфно подмножеству банахова пространства. А потом меня лень одолела и додумать следует ли из этого что-то хорошее я уже не смог :(

[Padawan]

Если метрическое пространство $X$ некомпактно, то на нем существует неограниченная непрерывная вещественная функция. Действительно, если пространство $X$ не полно (нам этот случай неинтересен, но всё же), то $X$ не замкнуто в своем пополнении $\hat X$. Пусть $x_0\in \hat X\setminus X$. Тогда функция $\varphi(x)=\frac{1}{\rho(x,x_0)}$ непрерывна и неограничена на $\hat X\setminus \{x_0\}$. Её сужение на $X$ будет искомой непрерывной неограниченной функцией. Если $X$ не вполне ограничено, то есть счётное семейство точек $\{a_i\}$ таких, что $\rho(a_i,a_j)\geqslant \varepsilon_0>0$ при $i\neq j$. 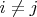Возьмём окрестности этих точек вида $U_i=B(a_i,\varepsilon_0/3)$ и для каждой такой окрестности рассмотрим функцию $\varphi_i(x)=\rho(x,X\setminus U_i)$. Функция $\varphi(x)=\sum_{i=1}^\infty i\varphi_i(x)$ будет искомой непрерывной неограниченной сверху функцией.
Итак, пусть $\varphi(x)$ -- неограниченная сверху непрерывная функция на $X$. Рассмотрим отображение $X$ в $X\times\mathbb R$, действующее по правилу $x\mapsto (x,\varphi(x))$. Это есть гомеоморфное вложение $X$ в $X\times\mathbb R$. Вообще, есть такая теорема, довольно очевидная: если $f\colon X\to Y$ -- непрерывное отображение топологических пространств, то $x\mapsto (x,f(x))$ есть гомеоморфное вложение $X$ в $X\times Y$, при этом, если $Y$ хаусдорфово, то образ $X$ при этом вложении замкнут в $X\times Y$.
Дальше я стал думать, как $X\times\mathbb R$ свернуть в конус так, чтобы $X\times\{+\infty\}$ свернулось в вершину конуса. И нашел в интернете такую интересную конструкцию, которая называется "евклидов конус над метрическим пространством". Если есть метрическое пространство $(X,d)$, то конус над $X$ есть фактор-пространство произведения $X\times\mathbb R_{\geqslant 0}$ с отождествлением $X\times \{0\}$ в одну точку. За расстояние между точками $(x,t)$ и $(y,s)$ принимается $\sqrt{t^2+s^2-2st\cos(\min \{d(x,y),\pi\})}$. То есть мы располагаем наше метрическое пространство на сфере единичного радиуса, и исходное расстояние $d(x,y)$ это угол между лучами, идущими из вершины конуса в точку $x,y$. Остроумно. Кстати, вычитал, я это в книжке

ex-math в сообщении #1405067 писал(а):

Есть полунаучпоп Деза, Деза "Энциклопедический словарь расстояний"

Так что реально она мне пригодилась. Там куча разных метрик. Русский перевод только плохой, однако.
Итак, вернемся к нашему $X$, которое мы вложили в $X\times\mathbb R$ виде множества $\{(x,\varphi(x))\mid x\in X\}$, причём функция $\varphi(x)$ неограничена сверху. Осталось вложить $X$ в упомянутый выше конус в виде множества $\{(x,e^{-\varphi(x)})\mid x\in X\}$. Это множество не содержит вершины конуса, но содержит точки, сколь угодно близкие к вершине. Значит это множество не замкнуто, значит не полно как метрическое пространство.

[Mikhail_K]

Спасибо!