Преобразование Фурье

[Men007]

Дана функция
$f(x)=\left\{ \begin{array}{rcl} 1, & 0<x\leqslant1\\ 0, & x>1\\ \end{array} \right.$. При этом также сказано, что она нечетная, то есть: $f(-x)=-f(x)$.
Найти образ Фурье данной функции.

Решение:

Образ (преобразование) Фурье $C(\omega)$ вычисляется по формуле: $C(\omega)=\frac{1}{\sqrt{2\cdot\pi}}\cdot\int\limits_{-\infty}^{+\infty}f(x)\cdot e^{i\cdot\omega\cdot x}dx$.

Согласно условию задачи имеем:

$C(\omega)=\frac{1}{\sqrt{2\cdot\pi}}\cdot\int\limits_{0}^{1}1\cdot e^{i\cdot\omega\cdotx}dx=\frac{1}{\sqrt{2\cdot\pi}}\cdot\int\limits_{0}^{1} (\cos(\omega\cdot x)-i\cdot \sin(\omega\cdot x))dx$.
Однако, так как функция является нечетной, то получим:
$C(\omega)=\frac{1}{\sqrt{2\cdot\pi}}\cdot\int\limits_{0}^{1} (-i\cdot \sin(\omega\cdot x))dx=\frac{i\cdot\cos(\omega)-i}{\omega\cdot \sqrt{2\cdot\pi}}$.
Верно ли я, опираясь на условие задачи, составил интеграл?

[svv]

Вы можете смело не писать точки в качестве знака умножения. В книгах по математике в таком качестве они используются очень редко (например, $3.75\cdot 4.67$).

В коде формулы после одной из точек \cdot Вы написали букву x вплотную, без пробела или другого разделителя, получилось \cdotx. Система восприняла cdotx как единую лексему (неизвестную ей), поэтому мы не видим там ни точки, ни $x$. Должно быть:
$C(\omega)=\frac{1}{\sqrt{2\pi}}\int\limits_{-\infty}^{+\infty}f(x) e^{i\omega x} dx$
C(\omega)=\frac{1}{\sqrt{2\pi}}\int\limits_{-\infty}^{+\infty}f(x) e^{i\omega x} dx

-- Вс ноя 05, 2017 18:38:00 --

Men007 в сообщении #1262526 писал(а):

сказано, что она четная

Men007 в сообщении #1262526 писал(а):

функция является нечетной

Определитесь, пожалуйста.

[Men007]

svv
Поторопился, там естественно нечетная будет функция.

[svv]

Men007 в сообщении #1262526 писал(а):

Однако, так как функция является нечетной, то получим:

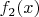
Тут Вы меняете смысл обозначения $C(\omega)$ в ходе рассуждения. Так делать нельзя. Сначала $C(\omega)$ соответствовало функции $f_1(x)$, которая равна $1$ на промежутке $(0,1]$, в остальных точках нулю. Такая $f_1(x)$ не будет ни чётной, ни нечётной. Потом $C(\omega)$ у Вас обозначает преобразование Фурье другой функции $f_2(x)$, которая нечётная и отлична от нуля на $[-1,0)\cup(0,+1]$.

Сначала надо явно задать функцию на всей области определения:
$f(x)=\left\{\begin{array}{rcl}1, & 0<x\leqslant 1\\-1,& -1\leqslant x<0 \\0, &\text{в остальных точках}\end{array}$
С ней и работать. Тогда и пределы интеграла будут другие, и вычислять его надо будет иначе, и результат будет другой.