Пусть

не имеет критических точек и уравнение

задает компактную

-поверхность

в

. Доказать, что при всех достаточно малых

уравнения

также задают компактные

-поверхности

, которые лежат в

-окрестности

и

при
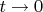
.
Естественно рассматривать

, где

--- ограниченная область (иначе утверждение попросту неверно).
Покажем, что

при
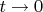
. Действуя от противного, найдем

и последовательность

такую, что

. В силу ограниченности, из

можно выделить сходящуюся к некоторому

. Тогда

и

. Противоречие.
Следствие. При достаточно малых

,

--- компактная

-поверхность в

. Компактность очевидна. Рассмотрим

. Тогда дифференциал

в точке

по условию имеет максимальный ранг, т. е.

. Тогда малым шевелением точки

эта максимальность сохранится. Далее применим компактность

и возьмем достаточно маленькие

, так чтобы

было малым, исходя из наименьшего радиуса конечного покрытия

. Тогда в точках

дифференциал

также имеет максимальный ранг, поэтому

--- компактная

-поверхность.
У меня возникли затруднения с тем, что

. В силу компактности, полурасстояние

между

и

достигается на элементах

и

. Тогда

Отсюда сразу видно, что

. Но дифференциал

необратим, поэтому неясно как получить нужное соотношение.