Теорема Хана-Банаха

[slimsaw]

Народ! Помогите! Нужно проиллюстрировать теорему Хана-Банаха в простейшем случае.
Функционал f задан на прямой, т.е. f отображает R1 в R1.
Надо продолжить этот функционал на пространство R2.
Нужно срочно!

[Narn]

Если коротко - нулем на ... ?

А вообще, задачка - тривиальнейшая. Так что, дабы не заработать с ходу замечание, прошу: 1) сформулировать теорему, 2) объяснить, что такое продолжение

[slimsaw]

Теорема.

Пусть L - линейное многообразие в банаховом пространстве X.
В L определён функционал f отображающий L в R1.
Тогда существует функционал g, отображающий X в R1, такой, что g(x) = f(x) при x принадлежащем L и норма g в X равна норме f в L

Добавлено спустя 3 минуты 58 секунд:

В данном случае L это прямая, т.е. R1. Значит f(x) = a*x. a - const
Продолжить функционал, значит построить новый функционал в новом пространстве. В данном случае в пространстве R2.

[Narn]

slimsaw писал(а):

Теорема.

Пусть L - линейное многообразие в банаховом пространстве X.
В L определён функционал f отображающий L в R1.
Тогда существует функционал g, отображающий X в R1, такой, что g(x) = f(x) при x принадлежащем L и норма g в X равна норме f в L

Пропущены 2 слова, причем одно я Вам подсказать могу - линейный (может, Вы других функционалов и не рассматривали), а вот пропуск другого превращает это из теоремы Хана-Банаха в простейшее утверждение.

slimsaw писал(а):

В данном случае L это прямая, т.е. R1. Значит f(x) = a*x. a - const

Хорошо, но у Вас прямая $R^1$ вложена в $R^2$. Будем считать, что это ось Ox. Тогда ее точки - это $(x_1,0)$, и, действительно, так как функционал линейный, то найдется константа $a$, такая, что

$f((x_1,0)) = ax_1$ для всех $x_1$.

slimsaw писал(а):

Продолжить функционал, значит построить новый функционал в новом пространстве. В данном случае в пространстве R2.

Не совсем верно. "Новое" пространство должно содержать в себе "старое" (на котором определен исходный функционал), а "новый" функционал должен совпадать со "старым" на его области определения.

[slimsaw]

Narn писал(а):

Пропущены 2 слова, причем одно я Вам подсказать могу - линейный (может, Вы других функционалов и не рассматривали), а вот пропуск другого превращает это из теоремы Хана-Банаха в простейшее утверждение.

Видимо второе слово - это ограниченный. Естественно я подразумевал, что f линеен и ограничен.

Narn писал(а):

Не совсем верно. "Новое" пространство должно содержать в себе "старое" (на котором определен исходный функционал), а "новый" функционал должен совпадать со "старым" на его области определения.

Само собой.

А как построить новый функционал?
В книгах написано, что нужно выбрать элемент x0, не принадлежащий L, рассмотреть новое множество L1 = (L0, x0) элементов вида u = x + t*x0, где x принадлежит L, t - любое действительное число.
Образуем новый функционал p(u) = f(x) - t*c, где c удовлетворяет некоторым условиям (каким именно сейчас не важно, главное что это действительное число).
А вот как построить функционал p в R2?
Ведь в R2 уже две координаты. Как это выражается формулой и какой будет график?
И ещё вопрос: единственно ли это продолжение?

[Narn]

Прошу прощения за мелкие придирки (ограниченность и продолжение). Это так, для уверенности.

А вот это

slimsaw писал(а):

А как построить новый функционал?
В книгах написано, что нужно выбрать элемент x0, не принадлежащий L, рассмотреть новое множество L1 = (L0, x0) элементов вида u = x + t*x0, где x принадлежит L, t - любое действительное число.
Образуем новый функционал p(u) = f(x) - t*c, где c удовлетворяет некоторым условиям (каким именно сейчас не важно, главное что это действительное число).
А вот как построить функционал p в R2?
Ведь в R2 уже две координаты.

уже плохо. Через $x_0, u, x$ у Вас обозначены векторы, а вовсе не их координаты. То есть $L_0 = \{ (a,0) | a \in \mathbb{R} \}$. Вот теперь выберите $x_0$ - вектор, не лежащий на Ox, и следуйте рецепту. Кстати, пользуйтесь тегом math, а не то тему в карантин отправят.

Добавлено спустя 3 минуты 12 секунд:

slimsaw писал(а):

Как это выражается формулой и какой будет график?
И ещё вопрос: единственно ли это продолжение?

Формулу Вы и должны написать. О графике пока говорить не хочется (это плоскость в трехмерном пространстве). Единственности, конечно, не будет.

[slimsaw]

Ну хорошо, вот выбрали в качество x0 какой-то вектор в произвольными координатами (x1, x2). Но в выражении для функционала p(u), f(x) зависит от одной переменной, t и c - действ. числа. А ведь p должен зависеть от двух переменных. В чём моя ошибка? Или f(x) в выражении для p(u) зависит от двух переменных?
И в выражении для u, как x0 имеет две координаты. Как x0 подставить в u?

Вы не могли бы написать эту формулу? Сам я что-то не могу сообразить.

(График - видимо плоскость, проходящая через начало координат)

[Narn]

slimsaw писал(а):

Ну хорошо, вот выбрали в качество x0 какой-то вектор в произвольными координатами (x1, x2). Но в выражении для функционала p(u), f(x) зависит от одной переменной, t и c - действ. числа. А ведь p должен зависеть от двух переменных. В чём моя ошибка? Или f(x) в выражении для p(u) зависит от двух переменных?
И в выражении для u, как x0 имеет две координаты. Как x0 подставить в u?

Во-первых, фиксируем на плоскости систему координат так, чтобы данная прямая была первой из координатных осей.

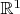
Функционал $f$ задан на прямой $\mathbb{R}^1$, вложенной в $\mathbb{R}^2$, то есть его аргументы - это векторы плоскости, лежащие на прямой. Любой вектор на плоскости имеет две координаты. Я не буду дальше обозначать векторы одной буквой, чтобы мы окончательно не запутались, только так: $(a,b)$. Векторы, лежащие на нашей прямой - тоже имеют две координаты, которые уже не произвольны: они должны удовлетворять уравнению данной прямой (при нашем выборе системы координат $x_2=0$).

Я ведь специально написал в очень корявом виде $f((x_1,0))$, чтобы подчеркнуть, что аргументом $f$ является один вектор. Вы, конечно, можете написать это покороче: $f(x_1,x_2)$ и говорить, что $f$ - функция двух переменных (числовых). Точно также и $p$ - то продолжение, которое мы хотим построить - функция одного вектора, но двух переменных. Разница между ними в области определения: в $p$ можно подставлять любой вектор, то есть выражение $p(x_1, x_2)$ определено при любых $(x_1, x_2)$, а в $f$ - только векторы нашей прямой (то есть вторая переменная должна быть 0). $f$ Вам дано, $p$ нужно придумать так, чтобы получился линейный (следовательно, ограниченный - почему?) функционал, норма которого равна норме $f$. Кстати, о чем я раньше думал!? - какая у Вас норма? Евклидова?

А вообще у меня ощущение, что я слишком много пишу. Посмотрите первое предложение первого моего поста в этой теме. Тогда даже на вопрос о норме можно не отвечать.