Добрый день. Необходимо вычислить приближенно
![$\sqrt[7] 3$ $\sqrt[7] 3$](https://dxdy-01.korotkov.co.uk/f/4/c/f/4cf770cc1fd2208705df606dd5309adc82.png)
с точностью до 0,001.
Пытаюсь привести
![$\sqrt[7] 3$ $\sqrt[7] 3$](https://dxdy-01.korotkov.co.uk/f/4/c/f/4cf770cc1fd2208705df606dd5309adc82.png)
к биномиальному ряду по принципу
![$\sqrt[n] A = \sqrt[n]{b^n +c} = \sqrt[n]{b^n \cdot (1 + c/b^n)} = b \cdot \sqrt[n]{1+c/b^n} = b \cdot (1 + c/b^n)^{1/n}$ $\sqrt[n] A = \sqrt[n]{b^n +c} = \sqrt[n]{b^n \cdot (1 + c/b^n)} = b \cdot \sqrt[n]{1+c/b^n} = b \cdot (1 + c/b^n)^{1/n}$](https://dxdy-01.korotkov.co.uk/f/4/7/e/47e1d97d6b26e1675a524d9bdde9db4c82.png)
, т.е.
![$\sqrt[7] 3 = \sqrt[7]{128 - 125} = 2 \cdot (1 - 125/128)^{1/7}$ $\sqrt[7] 3 = \sqrt[7]{128 - 125} = 2 \cdot (1 - 125/128)^{1/7}$](https://dxdy-03.korotkov.co.uk/f/2/b/e/2be969aa2fd8bd5a921189c79dfe285082.png)
Далее рассматриваю выражение

. Беру

, получаю биномиальный ряд

В общем случае


При

и
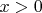
полученный ряд будет знакочередующимся, тогда останется доказать, что это - ряд Лейбница, и использовать оценку

для нахождения количества членов ряда, необходимых для вычисления с заданной точностью. Но у меня

, поэтому все члены ряда являются отрицательными, т.е. ряд не знакочередующийся и оценка

не применима.
Пробовал раскладывать в ряд

, но там опять не получалось знакочередования.
Раскладывал в логарифмический ряд, осуществив преобразование
![$\sqrt[7] 3 = e^\ln{\sqrt[7] 3}$ = 2 \cdot e^\ln{(1-125/128)^{1/7}} $\sqrt[7] 3 = e^\ln{\sqrt[7] 3}$ = 2 \cdot e^\ln{(1-125/128)^{1/7}}](https://dxdy-04.korotkov.co.uk/f/3/b/2/3b2fb7c4afa8b8e42dd5c4fde6856e7b82.png)
, но знакочередования опять не получилось.
Пытался привести подкоренное выражение к виду

так, чтобы

(
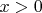
, чтобы было знакочередование,

, т.к. интервалом сходимости биномиального ряда является промежуток (-1; 1)). Получал

;
откуда

. Брал

Тогда

, но тут уже будет потеря точности и кажется, что должен быть более красивый вариант решения.
Как следует разложить подкоренное выражение, чтобы получить знакочередующийся ряд? Или есть что-нибудь, кроме признака Лейбница, что позволит оценить погрешность вычисления? Буду благодарен за высказанные идеи. Возможно, имеет значение, что ответом к заданию дано число 1,211, но
![$\sqrt[7] 3 \approx 1.167$ $\sqrt[7] 3 \approx 1.167$](https://dxdy-04.korotkov.co.uk/f/b/0/6/b06a5c07cde76450c7dcd16cc47397cf82.png)
, т.е. то ли в ответ, то ли в условие закралась ошибка