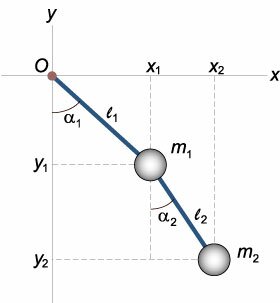
Рассмотрим двойной маятник в поле силы тяжести; невесомые стержни

и точечные массы

. Через

обозначим угол между вертикалью и

.
Обезразмерим задачу, приняв

.
Маятник запускают таким образом, что
начальные условия имеют вид

и

.
Доказать, что для любого сколь угодно малого

найдется такое

, что если

то при всех

будет

и

Если что, двойной маятник это вот что