почему нельзя свести задачу оптимизации с ограничения в виде неравенств к задаче в виде равенств
Почему же нельзя? Можно, так и делают. Я вот, кстати, не помню всех этих условий Каруша--Куна--Таккера и когда имею оптимизационную задачу с неравенствами, превращаю их в равенства и решаю полученную задачу уже привычным методом. Получается, я перевывожу известные вещи, ну и ладно, они благо не сложные.
Вам возможно кажется не совсем понятным появление условия неотрицательности множителей Лагранжа для условий-неравенств. В этом нет ничего сложного. Смотрите. Рассмотрим оптимизационную задачу

Введем фиктивные переменные

и рассмотрим равносильную задачу

Для простоты будем считать, что тут все скалярно и функции хорошие. Введем функцию Лагранжа

Тогда оптимальное решение этой задачи условной оптимизации удовлетворяет следующим необходимым условиям оптимальности первого порядка (это известный факт, принцип Лагранжа, мы им можем пользоваться):

Теперь покажем, что

не может быть решением этой задачи. Действительно, если

, то необходимо

, значит

. Получается, что оптимальное решение тогда обязано лежать на границе множества

. Но конкретно в данном случае эта точка не может быть оптимальной, потому что давайте рассмотрим точку

, где

,

. Из необходимых условий оптимальности мы видим, что

-- эта штука направлена внутрь множества

. Значит, при достаточно малом

мы найдем точку

получше, чем

для которой

. Значит, эта точка не может быть оптимальной, ибо мы знаем, что принцип Лагранжа устанавливает равносильность оптимальных точек исходной задачи условной оптимизации и безусловной оптимизации. Значит, как минимум

. Ну а там уже более конкретно и не скажешь, можно привести примеры, когда в оптимальной точке
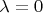
, и когда

.