Спасибо, смысл уловил.
Формально:
При

тем же интервалам принадлежит и

.
Тогда:

,

.
Сложив оба неравенства, получаем, что:
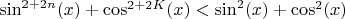
,
и, т.к.

, то при

уравнение не имеет решения.
Однако, уравнение имеет решение при

или

.
Спасибо.
-- 30.08.2017, 10:57 --А я было уже полез читать про бином Ньютона.