Кстати, актуальность задачи уж утрачена, так что можно и решение выложить.
Смотрим пристально на числитель и знаменатель. Первый начиная с некоторого числа (вычислять который нет надобности) монотонно идёт в плюс бесконечность при возрастании аргумента, а второй в любом промежутке вида

принимает минимальное значение

. Отсюда с необходимостью

, иначе решение неравенства есть. Но если

, то числитель должен быть строго положителен при любых

, иначе опять решение неравенства есть. Отсюда и вытекает ответ:
TOTAL писал(а):
Этот
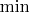
очевидно есть, но я его не вычислял и уж наверно он больше, чем

, иначе составителю было бы а-я-яй.