В тексте Декарта понятно почти всё, начиная со слов «я строю». Действительно, если построить всё так, как описано, получится, что «линия
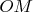
», то есть длина отрезка
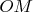
, равна приведённому выражению. Непонятно только, как это построение вытекает из исходного уравнения

.
Возможно, для Декарта это построение было графическим решением квадратного уравнения, но мне оно кажется подгонкой чертежа под известный алгебраический ответ.
Мессир, извольте объясниться!