Уравнение y^2=(n^4+1)(x^4+1)

[scwec]

Докажите, что уравнение $y^2=(n^4+1)(x^4+1)$ при любом рациональном $n$ имеет решение в рациональных числах $x,y$, отличное от $x=\pm{n},y=\pm{(n^4+1)}$.

[12d3]

И, видимо, отличное от $x=\pm{\frac{1}{n}},y=\pm{\frac{n^4+1}{n^2}}$?

[scwec]

Да, согласен. Отличное и от него тоже. Спасибо за бдительность. В условии лучше было написать решения вместо решение.

[scwec]

Привожу варианты нетривиальных ответов в рациональных числах $x,y$ для трех уравнений (где $n,k$ - рациональные числа)
$1.$ $y^2=(n^4+k)(x^4+k)$, в исходном уравнении $k=1$
$x=\dfrac{n(n^8-6kn^4-3k^2)}{3n^8+6kn^4-k^2}$
$y=\dfrac{(n^4+k)(n^{16}+28kn^{12}+6{k^2}{n^8}+28k^3{n^4}+k^4)}{(3n^8+6kn^4-k^2)^2}$

$2.$ $y^2=(n^3+k)(x^3+k)$
$x=\dfrac{n(n^3-8k)}{4(n^3+k)}$
$y=\dfrac{n^6+20kn^3-8k^2}{8(n^3+k)}$

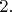
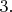
$3.$ $y^3=x(x+1)(x+n)$, $n\ne{0,1}$ (при $n=0,1$ имеем кривые рода $0$)
$x=-\dfrac{(2n-1)^3}{n^4+n^3+6n^2-14n+7}$
$y=-\dfrac{(n^2-1)(n-2)(2n-1)}{n^4+n^3+6n^2-14n+7}$

Все три уравнения соответствуют кривым рода 1 и приводятся к форме Вейерштрасса.
Для приведенных уравнений достаточно найти хотя бы одно рациональное решение бесконечного порядка (в данных случаях это не так сложно).
После возвращения к исходному виду получаются указанные решения.
Но так весело дела обстоят редко. Как правило, рациональные решения находятся не так просто и не для всех $n$.
Например, для уравнения $y^3=(x^3+1)(n^3+1)$ при $y\ne{0}$ рациональные решения находятся только (если рассматривать натуральные $n$) при $n=3,5,7,11,14,15,17,18,19,...$ всего 38шт. в пределах 100.
Решение при $n=3$ это, например, $x=-5/3, y=-14/3$.
При $n=5$ решения могут найти желающие.

[Levon]

Для уравнения $y^3=(x^3+1)(n^3+1)$ решение при $n=31$ это, например, $x=-41/59, y=1596/59$.

[scwec]

Levon, поскольку $N=31$ и ранг кривой в этом случае равен $2$, то к тому рациональному генератору, который Вы правильно вычислили $P(x,y)=(-41/59,1596/59)$ надо добавить и второй, независимый от первого: $Q(x,y)=(-365207473/398366767, 7561022868/398366767)$. Эти два генератора порождают все рациональные точки на кривой $y^3=(x^3+1)(31^3+1)$