задача Коши

[axeler44]

Добрый День

подскажите пожалуйста решение следующей задачи Коши:

$y' = x^3 \cdot y^2+ (2 - \frac{3}{x}) \cdot y - \frac{3}{x^3}$

1. Первым делом проверил данное уравнение на однородность, однородным оно не является, следовательно стандартной заменой $y = t \cdot x$ решить его не выйдет.

2. Зато является уравнением Бернулли (присутствует $y^n$)

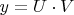
3. преобразовав уравнение и воспользовавшись заменой $ y = U \cdot V$ получил следующее:


$y' = y (x^3 \cdot y+ (2 - \frac{3}{x})) - \frac{3}{x^3}$

$\frac{U dV}{dx}$+$\frac{V dU}{dx} - UV \cdot ( x^3 \cdot UV + 2 - \frac{3}{x}) = - \frac{3}{x^3} $

для дальнейшего решения не смог вынести за скобки U или V.

подскажите пожалуйста, данный способ решения не верен, или необходимо дополнительно преобразовать выражение.

[Metford]

Я бы сначала отбросил первое слагаемое в правой части, решил уравнение - оно легко решается. Потом в полученном решении проварьировать константу. Прошёл бегло по решению - вроде бы всё нормально получается.

Да, и вот что...

axeler44 в сообщении #1229555 писал(а):

следующей задачи Коши:

У Вас не задача Коши, а просто уравнение.

[Ms-dos4]

axeler44
Во первых, это не уравнение Бернулли, это уравнение Риккати. Вам нужно найти любое частное решение ${y_0}$, удовлетворяющее данному уравнению и далее подстановкой $y = {y_0} + u$ вы перейдёте к уравнению Бернулли.
Metford
Не очень понял, как вы сумели сделать это.

[axeler44]

Metford в сообщении #1229563 писал(а):

У Вас не задача Коши, а просто уравнение.

1. Виноват, не дописал условие: $y(1)=1$.
Теперь задача Коши.

2. Если я правильно Вас понял мне следует поступить вот так:
немного не понял, про отбросить $x^3 \cdot y^2$

попробую перенести его в левую часть, сократить, вынести или иным способом преобразовать.

Спасибо за совет!

-- 25.06.2017, 19:26 --

Ms-dos4 в сообщении #1229569 писал(а):

axeler44
Во первых, это не уравнение Бернулли, это уравнение Риккати. Вам нужно найти любое частное решение ${y_0}$, удовлетворяющее данному уравнению и далее подстановкой $y = {y_0} + u$ вы перейдёте к уравнению Бернулли.

Ms-dos4
Большое спасибо!

[Metford]

Ms-dos4
Вы правы. Сейчас перепроверил - в конце расчёта пропустил переменную. Виноват. axeler44, извините.

Что-то я в последнее время невнимателен...

[пианист]

Уравнение здорово упрощается, если перейти к искомой функции $u=x^3y$