Пример правила подстановки

[root721]

Согласно книги правило подстановки

Цитата:

Если формула А доказуема в исчислении высказываний, х переменная, В произвольная формула исчисления высказываний. то формула. полученная в результате
замены в формуле А переменной х всюду. rде она входит,
формулой В, является также доказуемой формулой.
Операция замены в формуле А переменной х формулой В носит название подстановки и символически записывается так:

$\int\limits_{x}^{B} (A) $
Которая взаимодействует с группой аксиом, например.
$ x \to (x \to y) $
а) Если формула А есть переменная х, то подстановка дает В.
$ A \to (y \to A) результат B $
б) Если формула А есть переменная у. отличная от х, в то подстановка дает А
x \to (A \to x) результат A

в) Если А формула для которой подстановка уже определена то подстановка В вместо х в отрицание А есть отрицание подстановки.

Верно ли я написал а) и б)? Какой будет в)? Что означает подстановка уже определена? Как подстановка будет выглядеть в реальности?

[3D Homer]

Цитата из книги понятна. Все остальное непонятно.

root721 в сообщении #1225091 писал(а):

Которая

К чему относится "которая"? И вообще нехорошо начинать предложение с этого слова.

root721 в сообщении #1225091 писал(а):

взаимодействует

Что это значит?

root721 в сообщении #1225091 писал(а):

с группой аксиом, например.
$ x \to (x \to y) $
а) Если формула А есть переменная х, то подстановка дает В.
$ A \to (y \to A) результат B$

Какая подстановка? Напишите три составляющих подстановки, о которой идет речь.

[root721]

3D Homer в сообщении #1225213 писал(а):

К чему относится "которая"?

Правило подстановки которое взаимодействует с группой аксиом, например.

3D Homer в сообщении #1225213 писал(а):

Что это значит?

Я понял так, что правило подстановки описывает взаимодействие A, B и x с аксиомой.

3D Homer в сообщении #1225213 писал(а):

Напишите три составляющих подстановки, о которой идет речь.

Если а), б), в) не те составляющие, тогда о чём вы говорите?

[provincialka]

root721
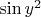
А вы понимаете, что такое подстановка, скажем, в алгебре? Если $A$ это $\sin x$, то подстановка $x=y^2$ превратит формулу в $\sin y^2$. Ну а если формула $A$ имеет вид $x$, то подстановка $x = B$ даст формулу $B$.
Более интересно делать подстановку не просто в формулу, а в тождество, тогдамы получим новые тождества-следствия.
Например, в тождестве $(x+1)^2=x^2+2x+1$ мы можем сделать подстановку $x=2t$, получим новое тождество $(2t+1)^2=(2t)^2+2\cdot 2t+1$

В этом примере роль формулы $A$ играет исходное тождество, $A : ((x+1)^2=x^2+2x+1)$

В вашем случае разница только в том, что вместо алгебраических формул берутся логические. Тогда, например, утверждение

root721 в сообщении #1225091 писал(а):

а) Если формула А есть переменная х, то подстановка дает В.

просто очевидно.

Вы в своих рассуждениях путаете формулы (видимо, предикаты? тут как-то неясно) и переменные (термы?)
Не надо подставлять куда-то $A$, разве что вы поменяете смысл исходных обозначений.

-- 14.06.2017, 09:04 --

И еще: знак равенства как знак подстановки лучше не использовать в логике, где он может иметь и другие смыслы. Поэтому его и заменяют на какой-нибудь значок (в ваших обозначениях -- интеграла). Например, в языке Паскаль присвоение обозначается знаком $:=$, то есть $x:=B$, а в языке $R$ -- знаком стрелки $x \leftarrow B$

[root721]

provincialka в сообщении #1225287 писал(а):

Вы в своих рассуждениях путаете формулы (видимо, предикаты? тут как-то неясно) и переменные (термы?)
Не надо подставлять куда-то $A$, разве что вы поменяете смысл исходных обозначений.

До предикатов я еще не дошел, они в следующей главе, я скорее путаю куда что подставлять. Особенно в случае в), что означает подстановка уже определена? Есть аксиома и есть подстановка, как она может быть уже определенной?

[provincialka]

Почему вы все время говорите про какую-то аксиому? В определении этого нет, и в ваших пунктах -- тоже.

А п. в) очень простой. Пусть вы уже сумели/научились подставлять $B$ вместо $x$ в $A$, получили формулу $C$. Тогда при подстановке $B$ в $\overline{A}$ вы получите формулу $\overline{C}$

Впрочем, я отвечаю из "общематематических" соображений, тонкостей не знаю. Например, что это за пункты а)-в): свойства, задаваемые нами или теоремы, которые надо доказывать?

(Оффтоп)

Мое столкновение с логикой было лет 40 назад, иипосле этого, слава богу, заниматься ею не приходилось

[root721]

provincialka в сообщении #1225365 писал(а):

Почему вы все время говорите про какую-то аксиому?

Они есть в книге, я так понял они взаимосвязаны с правилом подстановки или нет?

provincialka в сообщении #1225365 писал(а):

Например, что это за пункты а)-в): свойства

Свойства заданные правилами логики.
http://www.pm298.ru/ischisl.php

-- 14.06.2017, 16:13 --

Перечитал все заново, да вы правы. Аксиомы не взаимосвязаны.

[root721]

Хотя нет, дальше есть норм примеры и тут все ясно. Всётаки связаны.

[Z1X]

root721 в сообщении #1225091 писал(а):

в) Если А формула для которой подстановка уже определена то подстановка В вместо х в отрицание А есть отрицание подстановки.

Проще говоря, есть две унарные операции: подстановка и отрицание. То, что они коммутируют (без разницы, в каком порядке их выполнять), становится очевидно из синтаксических соображений: одна добавляет слева символ $\neg$, другая меняет переменную на формулу. Сам символ $\neg$ переменной не является и не может быть подставлен вместо переменной.

provincialka в сообщении #1225287 писал(а):

Вы в своих рассуждениях путаете формулы (видимо, предикаты? тут как-то неясно) и переменные (термы?)

Секунду! Речь ведь шла об исчислении высказываний? Строго говоря, термов там нет, а есть пропозициональные (логические, булевы) переменные и пропозициональные формулы. Конечно, в принципе можно сказать "логический терм", но это может запутать. В данном исчислении никто не запрещает вместо всех вхождений переменной вставлять целую формулу — в этом и состоит правило подстановки. Предикатов тут никаких нет

root721 в сообщении #1225383 писал(а):

http://www.pm298.ru/ischisl.php

и тут тоже. Но если говорить о логике предикатов, в ней появляются еще предметные переменные, и вот вместо предметных переменных формулы подставлять уже нельзя, а чтобы ввести новое правило подстановки нам действительно уже нужны термы.

Думается мне, автор этой темы не добрался еще до предикатной логики, и не стоит его торопить.

[arseniiv]

root721
Подстановка — это просто преобразование на формулах. Не важно, будем мы делать подстановку какой-то формулы вместо пропозициональной переменной в аксиоме или не аксиоме. Другое дело, что если мы делаем подстановку, например, в тождественно истинной формуле, результат тоже будет тождественно истинной формулой. Это не говорит ни о какой связи подстановки и аксиом, это просто отдельный факт.

-- Ср июн 14, 2017 22:24:34 --

(Оффтоп)

Кстати вот удивляюсь, что некоторые используют для обозначения какие-то $S_v^\psi(\varphi)$, когда есть вполне уже общепринятое $\varphi[\psi/v]$, у которого даже есть натуральное чтение «(подстановка в $\varphi$) $\psi$ вместо $v$» (достаточно запомнить, что $/$ = «вместо»).

[Z1X]

arseniiv в сообщении #1225479 писал(а):

есть вполне уже общепринятое $\varphi[\psi/v]$, у которого даже есть натуральное чтение «(подстановка в $\varphi$) $\psi$ вместо $v$»

Такая запись подстановки есть в пропозициональной логике?? Вы уверены?

-- 14.06.2017, 19:36 --

То есть это обозначение $\varphi[\psi/v]$ предписывает в формулу $\varphi$ вместо пропозициональной переменной $\psi$ подставить формулу $v$? Или наоборот?

[arseniiv]

(Оффтоп)

Наоборот. Чтение «$\psi$ вместо $v$», по-моему, однозначно.

Z1X в сообщении #1225528 писал(а):

Такая запись подстановки есть в пропозициональной логике?? Вы уверены?

А чем формулы и пропозициональные переменные хуже термов и предметных переменных? Не вижу причин делать две разные записи для одного и того же. Можно вообще отвлечься от логики и представить себе алгебру термов $m$ разных типов — так не рисовать же там $m$ разных замен!

[Z1X]

arseniiv в сообщении #1225546 писал(а):

А чем формулы и пропозициональные переменные хуже термов и предметных переменных? Не вижу причин делать две разные записи для одного и того же.

А потому что пропозициональная логика является частью предикатной. А в предикатной есть своя подстановка $\varphi[\psi/v]$ терма $\psi$ вместо предметной переменной $v$. В результате возникает путаница, когда одним и тем же способом обозначены разные подстановки. Тогда вообще из-за неоднозначности нельзя понять, что именно надо проделать с формулой.

Мне всегда казалось, что обозначение разных операций разными знаками — есть признак хорошего тона, и этого нужно придерживаться. Поэтому я бы одобрил исходное авторское обозначение $\int\limits_{x}^{B} (A)$ для этой подстановки.

[arseniiv]

(Оффтоп)

Z1X в сообщении #1225547 писал(а):

В результате возникает путаница, когда одним и тем же способом обозначены разные подстановки. Тогда вообще из-за неоднозначности нельзя понять, что именно надо проделать с формулой.

Ну здрасьте. Переменная не может быть одновременно пропозициональной и предметной. Уже по этому можно будет понять, какая подстановка имеется в виду. А вообще тип переменной не важен, а важно только то, чтобы вместо неё подставлялось нечто того же типа.

[Z1X]

(Оффтоп)

Надо точно знать что обозначают буквы латинского алфавита (в частности эта $v$). Это все определяется на уровне языка. И когда придет время строить предикатную логику на основе пропозициональной, надо будет менять язык.