Задача про интерференцию

[guitar15]

С помощью зрительной трубы, установленной на бесконечность, наблюдают интерференционные полосы в тонкой плоскопараллельной стеклянной пластинке толщиной $h=$ 0,2 мм с показателем преломления $n=1,41$; при этом угол наблюдения $\alpha$ может изменяться от 0 до 90° (рисунок снизу). Найти максимальный и минимальный порядок интерференционных полос. 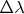Оценить допустимую немонохроматичность $\Delta\lambda$ источника, при которой будут достаточно четко
наблюдаться все интерференционные полосы. Каков допустимый размер источника света в этом интерференционном эксперименте? Используется зеленый свет
с длиной волны $\Delta\lambda=$ 560 нм.

Моя попытка решения:
Разность фаз для пленки определяется как
$\Delta=2h\sqrt{n^2-\sin^2{\theta}}$
Отсюда минимальная и максимальная разница фаз определяется как
$\Delta_{\min}=2h\sqrt{n^2-1}$
$\Delta_{\max}=2hn$
Отсюда
$m_{\max}=\frac{\Delta_{\max}}{\lambda}$
$m_{\min}=\frac{\Delta_{\min}}{\lambda}$
где, $m_{\max}$, $m_{\min}$ порядок.Допустимая немонохроматичность равна
$\Delta\lambda=\frac{\lambda}{m_{\max}}$
Проблема возникает в поиске допустимого размера источника по формуле.
$b=\frac{\lambda}{\Omega}$
где,$\Omega$ апертурный угол, $b$- допустимый размер.