Поверхностная и объемная плотность заряда

[iwndr]

Цитата:

Дан сферически симметричный потенциал электростатического поля:

$$\varphi(\vec{r})=\left\{\begin{matrix} 0 & r<R_0\\ \frac{c}{2} (r^2-R_0^2) & R_0\leq r \leq R_1\\ \frac{c}{2} (R_1^2-R_0^2) & r>R_1 \end{matrix}\right.$$

($c,R_0,R_1$ - постоянные отличные от нуля)

1) Найти $\vec{E}$ и объемную плотность $\rho(r)$.

2) Существуют ли области пространства в которых присутствует поверхностная плотность заряда? Если да, то опишите эти области и посчитайте плотности.

3) Найти заряд системы и посчитать ее энергию.

С математической точки зрения задача несложная. Очевидно, что

$$\vec{E}=\hat{r}\left\{\begin{matrix} 0 & r<R_0\\ -cr & R_0\leq r \leq R_1\\ 0 & r>R_1 \end{matrix}\right.$$

и

$$\rho=\left\{\begin{matrix} 0 & r<R_0\\ -3c\varepsilon_0 & R_0\leq r \leq R_1\\ 0 & r>R_1 \end{matrix}\right.$$

Интересен второй и третий пункт задачи. Поверхностная плотность заряда присутствует в $r=R_0$ и $r=R_1$ (именно там нарушается непрерывность поля). Эту плотность можно посчитать используя теорему Гаусса (нормальная составляющая поля должна меняться на $\sigma/\varepsilon_0$):

$$\sigma_{R_0}=-\varepsilon_0 c R_0 ~~,~~ \sigma_{R_1}=\varepsilon_0 c R_1$$

Причем, насколько я понимаю, в промежутке $R_0<r<R_1$ поверхностная плотность заряда равна нулю (отсутствует). Но тогда вопрос - как это сопоставить с тем, что в том же промежутке $\rho\neq 0$? Более того, получается что полный заряд системы нужно считать следующим образом:

$$Q=\oint \limits_{R_0} \sigma_{R_0} dA+\oint \limits_{R_1} \sigma_{R_1} dA+\int \rho dV$$

Оказывается, что $Q=0$. Что же получается? Есть некоторая незаряженная (но поляризованная?) сферическая оболочка толщины $R_1-R_0$ на поверхностях которой скопились заряды (отсюда и поверхностная плотность), причем знаки зарядов на внутренней и на внешней поверхностях противоположны. А внутри, получается, тоже есть заряды (ибо $\int \rho dV\neq 0$), но с другой стороны поверхностная плотность там отсутствует. Правильно ли я понял ситуацию?

[Munin]

iwndr в сообщении #1210881 писал(а):

Причем, насколько я понимаю, в промежутке $R_0<r<R_1$ поверхностная плотность заряда равна нулю (отсутствует). Но тогда вопрос - как это сопоставить с тем, что в том же промежутке $\rho\neq 0$?

А в чём проблема? Считайте объёмную и поверхностную плотности просто двумя независимыми слагаемыми в общем распределении заряда.

iwndr в сообщении #1210881 писал(а):

Более того, получается что полный заряд системы нужно считать следующим образом:

$$Q=\oint \limits_{R_0} \sigma_{R_0} dA+\oint \limits_{R_1} \sigma_{R_1} dA+\int \rho dV$$

Вообще в общем случае

$$Q=\sum\limits_{\substack{\text{по всем}\\ \text{точкам}}}q+\int\limits_{\substack{\text{по всем}\\ \text{линиям}}}\lambda\,dl+\int\limits_{\!\!\!\!\substack{\text{по всем}\\ \text{поверхностям}}\!\!\!\!}\sigma\,dS+\int\rho\,dV.$$

Ну а если залезете в теорию обобщённых функций, то будет просто $\int\rho\,dV,$ но в $\rho$ появятся слагаемые вида дельта-функций и их родственников и знакомых.

iwndr в сообщении #1210881 писал(а):

Оказывается, что $Q=0$. Что же получается? Есть некоторая незаряженная (но поляризованная?) сферическая оболочка толщины $R_1-R_0$ на поверхностях которой скопились заряды (отсюда и поверхностная плотность), причем знаки зарядов на внутренней и на внешней поверхностях противоположны.

Нет, вы пытаетесь слишком физическую интерпретацию придумать. А на самом деле, такая картина распределения зарядов - искусственная. Безо всяких поляризаций. Кто-то взял вещество с плотностью заряда. Слепил из него сферический слой. Кто-то взял поверхность, заряженную. И приделал её изнутри этого слоя. И другую - снаружи. Или просто кисточкой покрасил этот слой поверхностным зарядом - одним изнутри, другим снаружи. Не ищите глубокого физического смысла, это просто упражнение на расчёт, на умение обращаться с математикой.

[svv]

iwndr
Придумайте, пожалуйста, как можно было бы найти полный заряд системы, ничего не вычисляя.

[svv]

iwndr в сообщении #1210881 писал(а):

3) Найти заряд системы и посчитать ее энергию.

Парадокс. Опытных участников прошу не подсказывать.

В §37 «Теории поля» Ландау и Лифшиц доказывают, что следующие два выражения для электростатической энергии зарядов эквивалентны:
$U=\frac{1}{8\pi}\int E^2\;dV=\frac 1 2\int\rho\varphi\;dV$
Это в СГС. Интегрирование в обоих случаях по всему пространству.
Но в данной задаче эти выражения, очевидно, не равны. В первом интеграле подинтегральная функция неотрицательна ($E^2$), во втором — наоборот: $\varphi\geqslant 0, \rho\leqslant 0$. В чём тут дело?

[iwndr]

Munin в сообщении #1210889 писал(а):

А в чём проблема? Считайте объёмную и поверхностную плотности просто двумя независимыми слагаемыми в общем распределении заряда.
Вообще в общем случае

$$Q=\sum\limits_{\substack{\text{по всем}\\ \text{точкам}}}q+\int\limits_{\substack{\text{по всем}\\ \text{линиям}}}\lambda\,dl+\int\limits_{\!\!\!\!\substack{\text{по всем}\\ \text{поверхностям}}\!\!\!\!}\sigma\,dS+\int\rho\,dV.$$

Просто раньше не сталкивался с такой ситуацией. Трудно себе представить конфигурацию в которой поверхностная плотность отсутствует а объемная присутствует. Вроде в каждом слое этой сферической оболочки заряд присутствует (ибо $\rho\neq 0$), а с другой стороны поверхностная плотность отсутствует. На уровне ощущений выглядит странно.

Munin в сообщении #1210889 писал(а):

Нет, вы пытаетесь слишком физическую интерпретацию придумать. А на самом деле, такая картина распределения зарядов - искусственная. Безо всяких поляризаций.

Вы безусловно правы, что картина распределения зарядов искусственная. Мне всего лишь хотелось представить, как такая система выглядела бы в реальном мире.

svv в сообщении #1210898 писал(а):

Придумайте, пожалуйста, как можно было бы найти полный заряд системы, ничего не вычисляя.

Применить теорему Гаусса ко всей сферической оболочке? Поле вне оболочки равно нулю а значит и поток равен нулю, но тогда $Q=0$.

svv в сообщении #1210910 писал(а):

Парадокс. Опытных участников прошу не подсказывать.

Насколько я знаю оба выражения всегда равны. Еще раз посмотрел доказательство равенства - оно достаточно общее и не должно нарушаться в данном случае. В чем же все-таки дело? Спасибо.

[rustot]

iwndr в сообщении #1210946 писал(а):

Просто раньше не сталкивался с такой ситуацией. Трудно себе представить конфигурацию в которой поверхностная плотность отсутствует а объемная присутствует.

Под конечной поверхностной плотностью подразумевается бесконечная объемная плотность в бесконечно тонком слое, потому они (если не пользоваться обобщенными функциями) и разделяются на отдельные слагаемые. Если на поверхности нет такое бесконечно плотной пленки, то тогда достаточно просто объемной плотности, поверхность она тоже успешно захватывает

[svv]

iwndr в сообщении #1210946 писал(а):

Применить теорему Гаусса ко всей сферической оболочке?

Да, верно.

iwndr в сообщении #1210946 писал(а):

В чем же все-таки дело?

Пара предварительных замечаний.

1. Как Вы знаете, потенциал $\varphi(\mathbf r)$ определён с точностью до константы. Выбор того или иного потенциала из бесконечного множества функций, отличающихся константой, называется калибровкой. Пусть система зарядов финитна (вне некоторого шара зарядов нет), но суммарный заряд $Q$ ненулевой. Тогда, очевидно, изменение калибровки $\varphi\to\varphi+c$ приведёт к изменению значения интеграла:
$\frac 1 2 \int (\varphi+c)\rho\;dV=\frac 1 2 \int \varphi\rho\;dV+\frac 1 2 \int c\rho\;dV=\text{старое значение}+\frac c 2 Q$
ЛЛ при выводе существенно использовали то, что на бесконечности потенциал стремится к нулю — там, где отбрасывали объёмный интеграл с дивергенцией, сводящийся к интегралу по бесконечно удалённой поверхности. Так что формулу $U=\frac 1 2 \int \varphi\rho\;dV$ можно использовать лишь при $\varphi_\infty=0$, что и определяет правильную калибровку. В нашей задаче это не так.
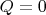
Однако парадокс этим не снимается, так как в нашем случае $Q=0$, и калибровка не должна влиять на результат.

2. Равенство $\frac{1}{8\pi}\int E^2\;dV=\frac 1 2\int\rho\varphi\;dV$ гарантируется только для интегралов по всему пространству, но для произвольной области интегрирования значения левой и правой части будут различны. Можно сказать, что «с точки зрения» первого и второго выражения электростатическая энергия локализована в пространстве по-разному. Вопрос об истинной локализации энергии (и её существовании) сложный и не должен сейчас обсуждаться. Сейчас предлагается просто считать, что оба интеграла имеют физический смысл $U$, лишь когда применяются ко всему пространству. Применять их к части пространства можно только в математическом смысле. Фраза
В этой области столько-то энергии с точки зрения выражения $\frac 1 2\int\rho\varphi\;dV.$
будет относиться лишь к аспекту вычисления.

Так вот, с точки зрения выражения $\frac 1 2\int\rho\varphi\;dV$ существенная часть энергии содержится на поверхностях. Об этом легко забыть. Коль вспомнили, как её учесть? Можно применить аппарат обобщённых функций, упомянутый Munin, тогда в выражение для $\rho$ на поверхностях будет входить дельта-функция. А можно догадаться, к чему сведётся дополнительное слагаемое «на человеческом языке»:
$\frac 1 2\int\limits_{\!\!\!\!\substack{\text{по всем}\\ \text{поверхностям}}\!\!\!\!}\sigma\varphi\;dS$
В нашем случае на внутренней поверхности потенциал нулевой. Зато «энергия» на внешней поверхности по модулю превосходит «энергию» непрерывного распределения и в сумме с ней даёт правильный результат. Вычисляется интеграл легко, так как на поверхности и $\sigma$, и $\varphi$ константы.

[iwndr]

Спасибо за пояснение.

svv в сообщении #1211016 писал(а):

ЛЛ при выводе существенно использовали то, что на бесконечности потенциал стремится к нулю

Речь идет об интеграле $\int \operatorname {div} (\varphi\vec{E})\, dV$? Но ведь его отбросили потому, что поле, а не потенциал, равно на бесконечности нулю (хотя, с математической точки зрения, главное чтобы хотя бы одна из этих величин обращалась в нуль на бесконечности). В нашем случае поле действительно равно нулю на бесконечности.

svv в сообщении #1211016 писал(а):

но для произвольной области интегрирования значения левой и правой части будут различны

Более того, для произвольной области $\frac{1}{8\pi}\int E^2\;dV$ не дает полную энергию системы, не так ли?

[svv]

iwndr в сообщении #1211029 писал(а):

Но ведь его отбросили потому, что поле, а не потенциал, равно на бесконечности нулю (хотя, с математической точки зрения, главное чтобы хотя бы одна из этих величин обращалась в нуль на бесконечности).

Пример того, сколько скрытых нюансов содержат книги ЛЛ.

Стремления поля к нулю на бесконечности мало. Возьмём случай одного точечного заряда $q$ в начале координат. Поле стремится к нулю как $r^{-2}$, но площадь поверхности шара с радиусом $r$ (поверхности интегрирования) растёт: $S=4\pi r^2$. Их произведение (поток поля) будет константой. Поэтому если ещё и потенциал не будет стремиться к нулю — то «капец».

iwndr в сообщении #1211029 писал(а):

Более того, для произвольной области $\frac{1}{8\pi}\int E^2\;dV$ не дает полную энергию системы, не так ли?

Не даёт полную. Но можно было бы надеяться, что даёт «частичную», содержащуюся в этой области. Но несовпадение таких частичных энергий области, даваемых $\frac{1}{8\pi}\int E^2\;dV$ и $\frac 1 2\int\rho\varphi\;dV$, хоронит эту надежду.

[iwndr]

svv в сообщении #1211036 писал(а):

Возьмём случай одного точечного заряда $q$ в начале координат. Поле стремится к нулю как $r^{-2}$

Да, но ведь это поле точечного заряда. В данной же системе поле не просто стремится к нулю при $r\to\infty$ - оно строго равно нулю для любого $r>R_1$.

Кстати, я нашел то о чем вы говорили у Сивухина: в §28 приводится уравнение (28.5) для энергии при любом распределении проводящих и диэлектрических сред в пространстве:

Цитата:

$$W=\frac{1}{2}\int \varphi \rho\; dV+\frac{1}{2}\int \varphi \sigma\; dS$$

Получается:

$$\frac{1}{2}\int \varphi \rho\; dV=\frac{-b^2 \pi \varepsilon_0}{5}(3R_1^5-5R_1^3 R_0^2+2R_0^5)$$

а также

$$\frac{1}{2}\int \varphi \sigma\; dS=\frac{1}{2}\left( \underbrace{\int \varphi(R_0) \sigma_{R_0}\; dS}_{=0}+\int \varphi(R_1) \sigma_{R_1}\; dS \right)=b^2 \pi \varepsilon_0 (R_1^5-R_1^3R_0^2)$$

что в сумме действительно дает $\frac{\varepsilon_0}{2} \int E^2 \; dV=\frac{2}{5}b^2 \pi \varepsilon_0 (R_1^5-R_0^5)$, как вы и говорили.

[Munin]

Ну, до какого-то места вполне можно верить, что $E^2/8\pi$ действительно даёт локализованную плотность энергии. Это удобный и яркий образ. А потом уже - прочитать про уточнения и нюансы. Это примерно так же, как то, что мы до какого-то момента воспринимаем $mgh$ просто как энергию, без оговорок.

[svv]

iwndr в сообщении #1211108 писал(а):

Да, но ведь это поле точечного заряда. В данной же системе поле не просто стремиться к нулю при $r\to\infty$ - оно строго равно нулю для любого $r>R_1$.

То, что такая мелочь, как «не та калибровка», выводит из строя формулу ЛЛ уже для случая сферически симметричного поля, я счёл достойным Вашего внимания. То, что при выводе отбрасывать поверхностный интеграл нельзя, если $Q\neq 0$ и $\varphi_\infty \neq 0$ (а, стало быть, нельзя и пользоваться полученной формулой для энергии) — интересно и важно само по себе.

В нашем случае $Q=0$, и поэтому, несмотря на неубывающий потенциал, калибровка на результат не влияет (а «парадокс» остаётся). Но ведь $Q=0$ — это же просто везение. Чуть в сторону — и всё.