Однако, написать "курс в задачах" оказалось делом небыстрым, вопреки ожиданию.
Если подходить к написанию его систематически, надо прежде всего изложить то, что называется "требования к подготовке
читателя". Главное: не предполагается никаких знаний, выходящих за рамки университетского курса общей и линейной алгебры.
Все дополнительные сведения, которые выходят за рамки, будут объяснены. Да и обязательный курс нужен лишь частично.
Скажем, теория Галуа или целые элементы в кольцах заведомо не нужны. Более всего нужны основные понятия о группах, кольцах
и алгебрах, многочленах, линейных преобразованиях, включая жорданову форму, и билинейных формах. Более точно описать, что
именно нужно, а что нет, затруднительно. Общая закономерность такая, что чем ближе к началу какого-либо учебника,
тем концентрация нужного выше. Есть много хороших книжек: Кострикин, Винберг, начало ван дер Вардена (из последнего
особенно гл.1--3), и много других. Они друг друга дополняют, что в одной не вполне удачно написано, может быть хорошо
изложено в другой. Кроме того, угол зрения и вообще строй мыслей в этих книгах разный, с этой точки зрения их тоже полезно
комбинировать. По линейной алгебре рекомендую еще Кострикин-Манина и Мальцева.
-- 21.03.2017, 18:19 --В общем, попробуем излагать более систематически.
1. Алгебры. Пусть

-- поле. Под
алгеброй над

понимается любое пространство над

, снабженное билинейным отображением

Никаких особых условий, кроме билинейности, на
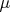
не предполагается. Вместо

обычно пишут
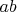
.
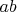
называется
произведением элементов

и

. Таким образом, билинейность эквивалентна соотношениям

для любых

,

. Вместо "для любых" говорят еще "тождественно по". Любое соотношение, верное для любых элементов алгебры, называется
тождеством в этой алгебре.
Примеры алгебр: 1) Само поле

. 2) Любое пространство

, если положить

для любых

и

(
алгебра с нулевым умножением).
3) Кольцо многочленов
![$K[x_1,\ldots,x_n]$ $K[x_1,\ldots,x_n]$](https://dxdy-04.korotkov.co.uk/f/7/1/2/712e5c8fcc55e1b7cf5676f60473d73d82.png)
от одной или нескольких переменных, относительно обычного умножения многочленов.
4) Кольцо
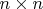
матриц над полем

, обозначаемое

, относительно обычного произведения матриц.
5) Множество векторов в обычном пространстве

, относительно операции векторного произведения

(основное поле --
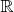
).
Поскольку произведение не предполагается ассоциативным (т.е., вообще говоря,

), то в сложных произведениях типа

нужно указывать расстановку скобок.
Алгебры, удовлетворяющие определенным тождествам, имеют специальные названия.
коммутативные алгебры:

;
антикоммутативные:

;
ассоциативные:

(значит, ассоциативная алгебра -- не что иное, как ассоциативное кольцо, которое одновременно является векторным пространством, причем операция умножения линейна по каждому аргументу);
альтернативные:

и

;
алгебры Ли: антикоммутативные алгебры, в которых вдобавок выполнено
тождество Якоби  йордановы
йордановы: коммутативные алгебры, удовлетворяющие тождеству

.
Замечание 1. Альтернативные и йордановы алгебры имеют отношение к алгебрам Ли (а именно, с их помощью строятся
простые алгебры Ли типов

и
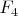
), но более подробно об этом сейчас писать неуместно, так как предмет весьма сложен. См.
М.М. Постников, Группы и алгебры Ли, лекции 14, 15, 16.
Задача 1. Показать, что тождество

влечет

,

. Если характеристика поля отлична от 2, то и обратно,

влечет

.
В дальнейшем мы будем предполагать, что основное поле -- характеристики 0, скажем

,
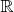
или

, а начиная с некоторого места --- что оно и алгебраически замкнуто. Алгебры Ли над полями простой характеристики --- предмет сложный. Над незамкнутыми полями -- даже над
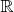
--- тоже непростой, сложней, чем над комплексным полем (я в этом предмете и не разбираюсь).
Замечание 2. Произведение в алгебре Ли обычно обозначается
![$[a,b]$ $[a,b]$](https://dxdy-04.korotkov.co.uk/f/f/e/4/fe477a2781d275b4481790690fccd15f82.png)
или
![$[ab]$ $[ab]$](https://dxdy-02.korotkov.co.uk/f/5/9/8/598767e35dbceaec8cf334033b3d18cc82.png)
. Но пока что удобно использовать обычное обозначение
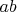
. (Да и вообще мы пока говорим об алгебрах вообще, а не специфически об алгебрах Ли).
Задача 2. Проверить, что векторы в трехмерном пространстве образуют алгебру Ли, над
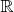
, относительно векторного умножения.
Размерность алгебры -- это её размерность как векторного пространства.
Задача 3. Пусть

-- одномерная алгебра с ненулевым умножением. Доказать, что существует базисный элемент

, для которого

. Таким образом,

изоморфна полю

, как алгебра.
Задача 4. Пусть

-- двумерная антикоммутативная алгебра с ненулевым умножением. Показать, что существует базис

, в котором

и

. Проверить далее, что

-- алгебра Ли.
Задача 5. В определениях разных типов алгебр выше все тождества были
однородны по каждой переменной. Например, в тождестве

, которое можно переписать как

, оба слагаемых имеют степень 2 по

и 1 по

. Это не случайно. Доказать, что если поле

бесконечно (в частности, если оно имеет характеристику

), и

--- тождество в

, то любая его однородная компонента -- тоже тождество. Например, если

--- тождество, то

,

, и

-- также тождества в

. Таким образом, любая совокупность тождеств эквивалентна некоторой совокупности (поли) однородных тождеств.
(Эта задача -- относительно сложная, и в дальнейшем не понадобится, но в общем полезная).
Пусть

-- алгебра. Элемент

такой, что

для всех

, называется
(двусторонней) единицей. Единицы может не быть. Например, в алгебре многочленов единица есть, а в произвольной алгебре с нулевым умножением -- нет.
Задача 7. Элемент

называется
левой единицей, если


, и
правой единицей, если


.
(а) Допустим, что

имеет левую единицу

и правую единицу

. Доказать, что

, и этот элемент является двусторонней единицей.
(б) Алгебра может иметь не более одной двусторонней единицы.
Пусть

, и

--- базис в

. Коэффициенты

в разложении

называются
структурными константами алгебры

.
Задача 8. Пусть

--- алгебра,

-- базис. В каждом случае доказать эквивалентность утверждений (i), (ii), (iii).
(а) (i)

коммутативна, (ii)

,


, (iii)

,

.
(б) (i)

антикоммутативна, (ii)

,


, (iii)

,

.
(в) (i)

ассоциативна, (ii)

,


, (iii)

,


.
(г) (i) В

выполнено тождество Якоби, (ii)

,


,
(iii)

,


.
Пусть

-- две алгебры. Отображение

--
гомоморфизм алгебр, если

линейно, и



.
Задача 9. (а) Если

,

,

-- три алгебры,

и

-- гомоморфизмы алгебр, то

-- тоже гомоморфизм.
(б) Если

,

, и

-- гомоморфизмы алгебр, то

.
Ясно, что тождественное отображение

-- гомоморфизм

в себя. Говоря короче, алгебры и их гомоморфизмы образуют
категорию. Согласно общекатегорным определениям, гомоморфизм

есть
изоморфизм, если существует гомоморфизм

такой,
что

и

.
Задача 10. (а) Пусть

,

-- две группы,

-- такое отображение, что



. Тогда

, где

-- единица в

,

-- в

, а также

(т.е., отображение между двумя группами, которое является гомоморфизмом полугрупп (без единицы), является на самом деле гомоморфизмом групп).
(б) Пусть

-- гомоморфизм групп, являющийся биективным отображением. Тогда обратное отображение

-- тоже гомоморфизм групп (так что

-- изоморфизм групп).
(в) Пусть

-- линейное отображение векторных пространств, биективное как отображение множеств. Тогда обратное отображение

также линейно.
(г) Пусть

-- гомоморфизм алгебр, являющийся биекцией. Тогда обратное отображение

тоже является гомоморфизмом алгебр (т.е., биективный гомоморфизм является изоморфизмом).
Задача 11. Две алгебры

,
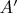
изоморфны тогда и только тогда, когда существуют базисы

в

и

в
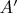
такие, что структурные константы алгебр

и
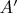
, соответственно, в этих базисах совпадают.
-- 21.03.2017, 18:39 --2. Подалгебры, идеалы, факторалгебры, прямые суммы. Пусть

-- произвольная алгебра,

-- произвольные подпространства. Через

обозначим подпространство, порожденное всеми произведениями

, где

,

. Сумма и пересечение подпространств определяется как обычно.
Задача 1. Пусть

-- произвольная алгебра,

-- подпространства.
(а) Доказать, что

,

.
(б) Доказать, что

. Привести пример, когда это включение строгое.
(Указание к (б))
Рассмотреть

как алгебру над
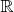
.
Если

, называем
 подалгеброй
подалгеброй, и обозначаем этот факт как

.
Левый (правый) идеал -- это подпространство

такое, что

(соответственно

); обозначение

,

, соответственно.
Двусторонний идеал -- это одновременно левый и правый идеал, обозначение

. Слово "идеал" без прилагательного означает двусторонний идеал.
Задача 2. (а) Если

, то

;
(б)



; аналогично для правых и двусторонних идеалов.
(в)

,



. Аналогично для правых и двусторонних идеалов.
Задача 3. (а) Если

, то

, и аналогично для правых и двусторонних идеалов.
(б) Если

,

, то

.
Задача 4. Допустим,

коммутативна или антикоммутативна. Тогда
(а)

для любых подпространств

;
(б) если

-- левый или правый идеал в

, то

-- двусторонний идеал.
Задача 5. Пусть

-- ассоциативная алгебра.
(а)

, для любых подпространств

.
(б) Если

,

, то

. Аналогично



.
(в)

,



.
(г)

,



.
Задача 6. Пусть

-- алгебра Ли.
(а) Для любых подпространств

.
(б)



.
Пусть

-- произвольная алгебра,

-- двусторонний идеал. На факторпространстве

определим умножение
по правилу

. Проверим, что это определение корректно, т.е. если

,

, то

.
Действительно, имеем

,

, для некоторых

. Тогда

. Но

,
значит

, откуда

.
Задача 7. Доказать, что умножение на

, определенное выше, билинейно; таким образом,

превращается в алгебру.
Пусть

,

-- две алгебры,

-- прямая сумма пространств. На

определим умножение как

.
Задача 8. Доказать, что относительно этого умножения

является алгеброй.

, с этой операцией умножения, обозначается

(
внешняя прямая сумма алгебр).
Задача 9. Пусть

-- алгебра,
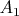
,
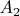
-- подалгебры в

такие, что

как пространство, и

. Тогда

. В последнем случае говорят, что

--
внутренняя прямая сумма своих подалгебр
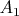
и
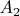
. С другой стороны, если

-- внешняя прямая сумма алгебр
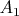
и
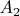
,
то подпространства

и

-- подалгебры в

, и

-- внутренняя
прямая сумма

и

.
Задача 10. (а) Если в алгебре

выполнено некоторое тождество, то в любой подалгебре и в любой факторалгебре выполнено то же тождество.
(б) Если в обоих алгебрах

и

выполнено тождество (одно и то же в обеих), то в

выполнено то
же тождество.
Задача 11. Пусть

-- гомоморфизм алгебр,

-- его ядро,

--
образ. Доказать, что (а)

, (б)

.
Задача 12. Пусть

-- гомоморфизм алгебр.
(а) Если

, то

.
(б) Если

, то

(здесь

-- полный прообраз).
(в)



; аналогично для правых и двусторонних идеалов.
(г) Если

сюръективно, и

, то

. Аналогично для правых и двусторонних идеалов.
Задача 13. Доказать, что левые идеалы в

-- это в точности подпространства вида

, где

,

. Аналогично для правых и двусторонних идеалов.