Серия задач, которая подводит к доказательству квадратичного закона взаимности.
а) Определить количество решений уравнения

в поле
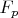
.
Перенеся один квадрат вправо, получил, что решениями будут корни из таких вычетов

, что

также являются вычетами. То есть пригодится сумма

. Просмотрев несколько первых p (7, 11, 13, 17) получается ответ p+указанная сумма.
Вообще, проходим сейчас квадратичные формы. Поэтому, скорее всего, надо их применить.
Может кто помочь?