Задача: На пути тележки массой

, скользящей по гладкому горизонтальному столу со скоростью

, находится незакрепленная горка высотой

и массой

. Тележка по горке, а также горка по столу скользят без трения. Скорость тележки

недостаточна, чтобы преодолеть горку. На какую максимальную высоту

поднимется тележка? Какие скорости

и

приобретут тележка и горка, когда тележка съедет с горки, не добравшись до вершины.
Решение:
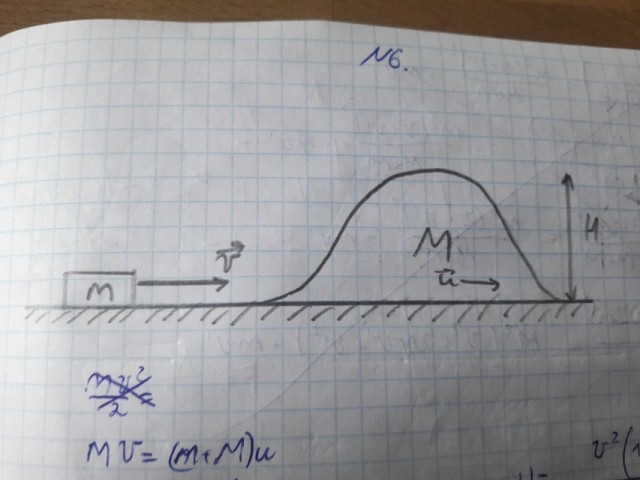
Пусть

- скорость горки при "столкновении" тележки с горкой.
Импульс в системе сохраняется, поэтому
![$\[mv = (m + M)u\]$ $\[mv = (m + M)u\]$](https://dxdy-01.korotkov.co.uk/f/4/c/3/4c3255029a9d56dda3310946eb36d35282.png)
, откуда
![$\[u = \frac{{mv}}{{m + M}}\]$ $\[u = \frac{{mv}}{{m + M}}\]$](https://dxdy-04.korotkov.co.uk/f/7/d/7/7d78285f3387eb558942930281b8b81182.png)
. Далее, распишем закон сохранения энергии для этого случая:
![$$\[\frac{{m{v^2}}}{2} = mgh' + \frac{{m{u^2}}}{2}\]$$ $$\[\frac{{m{v^2}}}{2} = mgh' + \frac{{m{u^2}}}{2}\]$$](https://dxdy-04.korotkov.co.uk/f/7/9/0/790399686d13e2a9b7a3654f6f91b46782.png)
![$$\[\frac{{m{v^2}}}{2} = mgh' + \frac{{m{{\left( {\frac{{mv}}{{m + M}}} \right)}^2}}}{2}\]$$ $$\[\frac{{m{v^2}}}{2} = mgh' + \frac{{m{{\left( {\frac{{mv}}{{m + M}}} \right)}^2}}}{2}\]$$](https://dxdy-03.korotkov.co.uk/f/e/2/1/e216e2a00c6a7bafa0392ea69ae5df6f82.png)
Откуда:
![$$\[h' = \frac{{{v^2}\left( {1 - \frac{{{m^2}}}{{{{\left( {m + M} \right)}^2}}}} \right)}}{{2g}}\]$$ $$\[h' = \frac{{{v^2}\left( {1 - \frac{{{m^2}}}{{{{\left( {m + M} \right)}^2}}}} \right)}}{{2g}}\]$$](https://dxdy-04.korotkov.co.uk/f/f/d/2/fd2c050e6212ed1f19aab44a497e5d0a82.png)
Теперь рассмотрим такую систему: пусть тележка стоит на неподвижной горке на высоте
![$\[{h'}\]$ $\[{h'}\]$](https://dxdy-03.korotkov.co.uk/f/6/2/2/6220833fbba39c1f35e1e4d22b8024ae82.png)
, трения нигде нет.
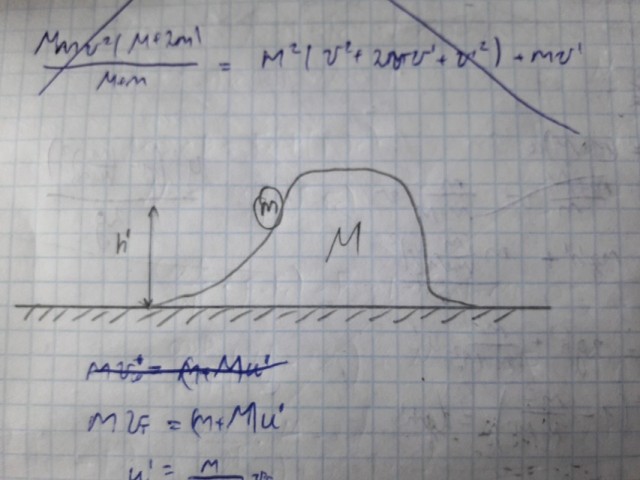
Ясно, что когда когда тележка съедет с горки, то ее скорость будет равна

. Пусть

- скорость горки после спуска тележки. Тогда

. Согласно закону сохранения импульса:
![$$\[m{v_g} = (M + m)u'\]$$ $$\[m{v_g} = (M + m)u'\]$$](https://dxdy-03.korotkov.co.uk/f/6/8/1/6816775587d3cb8b943b2e2fe37d57e282.png)
, откуда
![$\[u' = \frac{{m{v_g}}}{{m + M}}\]$ $\[u' = \frac{{m{v_g}}}{{m + M}}\]$](https://dxdy-01.korotkov.co.uk/f/4/4/d/44d77a68267de31b36983104a48964eb82.png)
. Закон сохранения полной мех. энергии для данного случая будет иметь вид:
![$$\[mgh' = \frac{{(M + m){{u'}^2}}}{2} + \frac{{m{v_g}^2}}{2}\]$$ $$\[mgh' = \frac{{(M + m){{u'}^2}}}{2} + \frac{{m{v_g}^2}}{2}\]$$](https://dxdy-02.korotkov.co.uk/f/5/f/d/5fddf78baa113174c256a9f78ebf510a82.png)
После подстановки туда

и

и применения формулы разности квадратов получим
![$\[{v_g} = v\sqrt {\frac{M}{{m + M}}} \]$ $\[{v_g} = v\sqrt {\frac{M}{{m + M}}} \]$](https://dxdy-01.korotkov.co.uk/f/4/b/0/4b086e3fdce021798835621cabbb5fee82.png)
![$\[{u_t} = u + u' = \frac{m}{{m + M}}(v + {v_g}) = \frac{{mv}}{{m + M}}\left( {1 + \sqrt {\frac{M}{{m + M}}} } \right)\]$ $\[{u_t} = u + u' = \frac{m}{{m + M}}(v + {v_g}) = \frac{{mv}}{{m + M}}\left( {1 + \sqrt {\frac{M}{{m + M}}} } \right)\]$](https://dxdy-01.korotkov.co.uk/f/c/b/4/cb45d02bebffb9955e2544353d2ae78782.png)
Проблема в том, что скорости не зависят от

, которая дана в задаче.