Теорема об изоморфности простого подполя

[wedneses]

Доброго времени суток

Хотелось бы разобраться в следующей теореме (учебник Кострикина, Введение в алгебру 1)

Цитата:

1) В каждом поле $P$ содержится одно и только одно простое поле $P_0$.
2) Это простое поле изоморфно либо $\mathbb{Q}$, либо $\mathbb{Z}_p$ для некоторого простого $p$.

Здесь под $\mathbb{Z}_p$ понимается кольцо класса вычетов.

Итак, я полностью разобрался с пунктом 1). 2) же добить не получилось.

В учебнике предлагается следующее доказательство.

Цитата:

1) В $P_0$ наряду с единичным элементом $1$ содержатся все его кратные $n\cdot 1 = 1 + ... + 1$.

2) Из общих свойств операций сложения и умножения элементов в кольцах следует, что $s \cdot 1 + t \cdot 1= (s + t) \cdot 1, \; (s \cdot 1 ) (t \cdot 1) = (st) \cdot 1; s, t \in \mathbb{Z}$

3) Поэтому отображение $f$ кольца $\mathbb{Z}$ в $P$, определённое правилом $f(n) = n \cdot 1$, является гомоморфизмом, ядро которого имеет вид $\operatorname{Ker} f = m\mathbb{Z}$.

4) Если $m=0$, то $f$ — мономорфизм, и дроби $\frac{(s \cdot 1)}{(t \cdot 1)}$, имеющие смысл в $P$ (поскольку $P$ — поле), образуют поле $P_0$, изоморфное $\mathbb{Q}$. Оно и будет простым подполем в $P$.

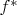
5) Если же $m > 0$, то, очевидно, отображение $f^*$, определённое по правилу $f^*: \bar{k} = \{k\}_m \mapsto f(k)$ будет изоморфным вложением $\mathbb{Z}_m \to P$.

6) Это возможно только тогда, когда $m = p$ — простое число.

7) Стало быть, $f^*(\mathbb{Z}_p)$— простое подполе в $P$.

Я, кажется, разобрался с 1), 2) - довольно очевидные.
3) $f(n + m) = (n + m) \cdot 1 = n \cdot 1 + m \cdot 1 = f(n) + f(m)$, аналогично $f(nm) = f(n) f(m)$ - с этим вроде все хорошо. У Кострикина появляется $m$ - я так понимаю, что это индекс кольца вычетов $\mathbb{Z}_m$. (до этого $m$ только для этого и использовалось)
4) Согласен, что при $m = 0 \Rightarrow \operatorname{Ker} f = 0$ и $f$ - мономорфизм. Далее появляется дробь $\frac{s \cdot 1}{t \cdot 1}$, и мне непонятно, каким образом $f$ станет изоморфизмом. Т.е. тогда должно имется в виду, что $f(n m) = \frac{f(n)}{f(m)} = \frac{n \cdot 1}{m \cdot 1}$?
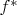
5) Отображение $f^*$ берет класс вычетов $\bar{k}$ и ставит ему в соответствие что? $f(k)$, где $k$ - единственный представитель $\bar{k}$ (т.е. один элемент $f(k) = k \cdot 1$? Или $f(k)$ возвращеает множество $\{l \cdot 1 | l \in \bar{k}\}$ - тотатльное непонимание.
6) Несмотря на то, что я совсем не понял пункт 5), с 6) я почему-то разобрался. Т.е. если бы $m$ было составным, то в нем были бы делители нуля, т.е. не каждый элемент был бы обратим, а изоморфизм сохраняет обратимость ($f(a^{-1}) = f(a)^{-1}$).

Очень хотелось бы разобраться с этим доказательством. Буду рад любой помощи.

[Brukvalub]

wedneses в сообщении #1187999 писал(а):

4) Согласен, что при $m = 0 \Rightarrow \operatorname{Ker} f = 0$ и $f$ - мономорфизм. Далее появляется дробь $\frac{s \cdot 1}{t \cdot 1}$, и мне непонятно, каким образом $f$ станет изоморфизмом.

Дроби не имеют отношения к $f$. Они появляются, чтобы сказать, каким будет простое подполе.

wedneses в сообщении #1187999 писал(а):

5) Отображение $f^*$ берет класс вычетов $\bar{k}$ и ставит ему в соответствие что? $f(k)$

Да. Дело в том, что есть теорема: факторкольцо кольца по ядру гомоморфизма изоморфно образу этого кольца при действии гомоморфизма. Вот эта теорема в данном случае и используется.

[wedneses]

Brukvalub

0) Если в $P_0$ содержатся все $\dots, -1, 0, 1, 2, \dots$, то наряду с ними содержатся и обратные $\frac{1}{1}, \frac{1}{2}, \dots $
1) Если у нас $P_0$ изоморфно $\mathbb{Q}$, то должно существовать отображение $g: \mathbb{Q} \to P_0$, где $g(q_1 + q_2) = g(q_1) + g(q_2), \; g(q_1 \cdot q_2) = g(q_1) g(q_2)$ и $g$ биективно.
2) Учитывая 0), мне становится понятно, что $g$ существует, но прочитанном мной доказательстве я ничего такого не нашел. Т.е. $f$ там выполняет не совсем понятную мне задачу.
3) Можно, если не сложно, поподробнее объяснить про $f^*$? Т.е. факторкольцо кольца по ядру гомоморфизма - это объединение классов $\bar{0}, \dots, \overline{m - 1}$. Образ кольца при действии гомоморфизма - это просто $m$ чисел $0, 1, \dost, m - 1$?

[Brukvalub]

wedneses в сообщении #1188015 писал(а):

Т.е. $f$ там выполняет не совсем понятную мне задачу.

Чтобы понять роль $f$ попробуйте придумать свое, альтернативное док-во теоремы, не опирающееся на $f$.

wedneses в сообщении #1188015 писал(а):

3) Можно, если не сложно, поподробнее объяснить про $f^*$? Т.е. факторкольцо кольца по ядру гомоморфизма - это объединение классов $\bar{0}, \dots, \overline{m - 1}$. Образ кольца при действии гомоморфизма - это просто $m$ чисел $0, 1, \dost, m - 1$?

Не уверен, что в исходном поле вообще есть числа $0, 1, \dost, m - 1$, их роль могут играть, скажем, пивные кружки.

[vpb]

wednesses,
попробуйте сделать следующее. Вернитесь на несколько страниц назад в Кострикине. Там написано, вполне ясно и с доказательством, как производить действия с "дробями" в произвольном поле. А затем, закрыв книжку, попробуйте сами доказать, что если в поле $2\cdot1\ne0$ и $3\cdot1\ne0$, то $(1\cdot1/2\cdot1)+(2\cdot1/3\cdot1)=7\cdot1/6\cdot1$
(именно доказать, а не посчитать, как в школе). Как это сделаете --- сразу поймете, почему с выражениями $p\cdot1/q\cdot1$ можно оперировать так же, как с обычными дробями (при условии, конечно, что поле --- характеристики 0, т.е. $n\cdot1\ne0$ при $n\ne0$). Это и значит, что такие элементы образуют
подполе, изоморфное $\mathbb Q$.

(Оффтоп)

А вообще, Кострикин --- отличный учебник, достаточно его просто вдумчиво и неторопливо изучать, особо во время семестра, а не впопыхах к пересдаче.

[wedneses]

Разобрался, спасибо.

(Оффтоп)

К слову, я как раз и изучаю Кострикина, неторопливо (потому что туплю) и в во время семестра, не к пересдаче