daogiauvangОт противного: пусть у любой пары - нечетное число общих знакомых.
Пусть

- знакомые

, а

- незнакомые.
1. Пусть
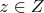
. Тогда для

условие "

знаком с

" равносильно тому, что

- общий знакомый для

. Поэтому

знаком в группе

с нечетным кол-вом чел. Значит,

-четно (число нечетных вершин подграфа

- четно). Тогда

- нечетно.
Значит, каждый

знаком с четным кол-вом чел.
2. Каждый из

знаком с

, в группе

имеет нечетное число знакомых, и общее число его знакомых - четно (по п. 1). Значит, у каждого из них - четное число знакомых в группе

.
Значит, из

в

идет четное число ребер.
3. Пусть

. У них с

- нечетное число общих знакомых, и все они - в группе

. Значит, из каждой вершины

в группу

идет нечетное число ребер. Но в группе

нечетное число чел.
Значит, из

в

идет нечетное число ребер.
Противоречие с 2.