About the problem from Israel - it can be proven from
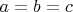
that

is equilateral.
I also have proofs for the facts
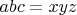
and
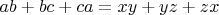
but don't know how to proceed further.
For a=84, b=35, c=40 I'm capable to solve the problem in 3 ways, but for the common case using software I found 2 kilometer long roots exist. It is the reason to wonder is there something simpler as an expression.
If we denote the ratios in which the cevians divide the triangle's sides with

,

,

and the areas are

,

,

the following system is correct:
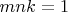
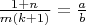
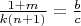
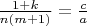
but again ugly 4-th degree equations can be found.
I wonder if we express the ratios
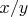
,
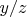
,
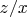
where

,

,

are the unknown areas in terms of

,

,

and try to eliminate

,

,

what will happens.