
Вроде всё пока правильно. Один из возможных путей: выразить

из второго уравнения, и подставить в первое. Получится уравнение на

, которое должно решаться в натуральных числах. Его общее решение находится алгорифмом Евклида, а частное, которое интересует нас, из условия
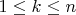
.

— становится сразу понятен.