Наверное, им задача неинтересна

. Посему предложу свое решение.
Для начала ослабим условие задачи, заменив
![$\mathbb{Q$$[x]}$ $\mathbb{Q$$[x]}$](https://dxdy-01.korotkov.co.uk/f/c/3/8/c38ba32a231de072396f6741dd2da16382.png)
на
![$\mathbb{Z$$[x]}$ $\mathbb{Z$$[x]}$](https://dxdy-02.korotkov.co.uk/f/9/0/2/90282f6b06d1c3a851a36422835e0ffb82.png)
. Тем самым мы упростим рассуждения, да и основная конструкция доказательства станет более воспринимаемой. Возврат к исходным условиям произведем чуть позже (писанина с тегами с непривычки отнимает у меня много времени) - там все рассуждение подвергнется небольшой модификации.
Докажем, что кроме полиномов

, других полиномов с условиями 1, 2 не существует.
Опущу банальный случай

- здесь все очевидно: решения -

.
Пусть
 ___________
___________(*)
- полином, удовлетворяющий условиям 1, 2.
Далее нам понадобится простенькая
Лемма Если

, то

.
Доказательство леммы тривиально: подставляем

в представление (*), раскрываем все биномы, отделяем все слагаемые, делящиеся на

и видим, что оставшиеся слагаемые дают в сумме

.
Приступим к основной задаче.
Из условия 1 вытекает, что

. Запомним это.
Пусть

.
Пусть

, обеспечивает выполнение условия 2. В силу конечности числа корней у полиномов и бесконечности множества простых чисел существует простое число

, для которого

,

и

. Отсюда следует, что

и, следовательно,

. Но, согласно
лемме,

. Т.е. для пары

имеем

и

, что означает (ввиду

), что

и

не взаимно-просты. Мы пришли к противоречию с п. 2. Таким образом, мы доказали, что среди полиномов с

и

искомых полиномов не существует.
Пурист бы указал здесь на пробел в рассуждении: не рассмотрен случай, когда

(тогда не выполняется требование

). Но, полагаю, пурист в состоянии сам в этом случае вместо полинома
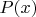
расмотреть полином

.
Пусть теперь

.
Тогда либо

, либо для некоторого

имеем

, где у полинома

свободный член

отличен от нуля.
В первом случае легко убедиться, что полином удовлетворяет условию п.2 лишь при

, что мы и отражаем в ответе.
Во втором случае опять возьмем простое

, для которого

,

и

. Наличие таких чисел обосновывается точно также, как и выше. Из выбора

вытекает, что

и, следовательно,

.
Вычислим теперь

:


(буквами

и

обозначены суммы членов, образующихся при раскрытии биномов - как и при доказательстве леммы - в

и

соответственно). Теперь сразу видно, что

, т.е.

(помня, что

). Вот мы и пришли к противоречию с п.2. Доказательство завершено.
Осталось вернуться к исходной .
Излагать решение для исходной, редакции задачи (![$P\in\mathbb{Q$$[x]}$ $P\in\mathbb{Q$$[x]}$](https://dxdy-02.korotkov.co.uk/f/9/d/3/9d37ffb6979350d7d9642d5e9d2a136182.png) ), по-видимому нет смысла, поскольку Руст итак его знает, а остальные заинтересованные читатели (коих не наблюдается) в состоянии самостоятельно, полагаю, воспроизвести его
), по-видимому нет смысла, поскольку Руст итак его знает, а остальные заинтересованные читатели (коих не наблюдается) в состоянии самостоятельно, полагаю, воспроизвести его 
.