Доказать примитивную рекурсивность функции

[Pearl Jam]

Здравствуйте. Помогите, пожалуйста, в следующем деле.
Схема примитивной рекурсии для функции n переменных выглядит следующим образом:
$f(x_1,x_2,...,x_n,0)=g(x_1,x_2,...,x_n)$
$f(x_1,x_2,...,x_n,y+1)=h(x_1,x_2,...,x_n,y,f(x_1,x_2,...,x_n,y))$

Проблема заключается в том, что мне нужно доказать примитивную рекурсивность функции $f(x)=x^2.$
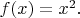
Но это функция от одной переменной. Выходит, что если мы, согласно формуле (1) приравниваем к нулю её последний аргумент (он же единственный), получается, функция g вообще не имеет аргументов. Я не могу понять, как применять схему к функциям от одной переменной.

[Xaositect]

Функция от нуля переменных - это константа. Соответственно, примитивная рекурсия для одной переменной будет
$\begin{cases}f(0) = c\\ f(y + 1) = h(y, f(y))\end{cases}$
В учебниках обычно отдельно ее пишут, там тоже почему-то не любят функции с нулем аргументов.

[Pearl Jam]

Спасибо, именно то, что я искал!