бессмысленность континуум-гипотезы

[маткиб]

Хорошо известен факт, что континуум-гипотеза (несуществование промежуточной мощности между счётным и континуумом) независима с ZFC (если ZFC такая, сякая, очень хорошая...). Но например вот тут

http://kosilova.textdriven.com/narod/st ... IRUSES.PDF
(pdf, 117KB, не реклама)

имеет место такая

Цитата:

Математики слышали о неразрешимых проблемах, но по-прежнему верят в давно поверженного идола "математической истины" и слепо поклоняются ему. До сих пор в работах ведущих математиков встречаются вопросы типа "Ну да, мы слышали, что гипотеза континуума неразрешима. Но на самом деле истинна она или нет?" Стоит накрепко запомнить, что сама постановка вопроса об истинности утверждения в теории множеств абсурдна.

Конечно, я соглашусь, что постановка вопроса об истинности в теории множеств абсурдна, но причина этого, по-моему, всё-таки в том, что мы не можем однозначно (чтобы все были согласны) определить, что считать множеством, а что нет. Кроме того, для того, чтобы хоть как-то неформально определить, что такое множество, нужно построить модель ZFC (т.е. уже выйти из ZFC), а потом её ещё и однозначно зафиксировать.

Но из цитаты Непейводы вроде как следует, что абсурдна даже истинность таких высказываний, как континуум-гипотеза. Хотя тут уж не должно быть никаких проблем: рассматриваем только множества последовательностей из нулей и единиц, да и дело с концом, в терминах таких множеств можно сформулировать континуум-гипотезу. В чём я не прав? Или автор цитаты (Непейвода) просто слишком уверен, что "в природе бесконечностей не бывает"?

[MaximKat]

Как-то меня смутили ссылки на библию в последнем разделе. А все так хорошо начиналось... Только что заметил, там еще и Норбеков есть
Я вот другого не понял: при построении множества Витали, он пишет что использует ZF, а потом удивляется, как же это мы выбираем элементы из множеств. Написал бы сразу, что используем ZFC и не пришлось бы удивляться.
Дальше,

Цитата:

В 1968 г. Р. Соловей доказал, что в стандартной теории множеств нельзя явно построить ни одного измеримого множества... Но данный факт отнюдь не влечет того, что любое явно построенное множество измеримо

Тут автор противоречит сам себе. Если неизмеримое множество явно построить нельзя, то логично, что явно построенное множество измеримо. Другое дело, что результат Соловья утверждает совсем другое, а именно, что утверждение о измеримости всех явно построенных множества совместимо с ZFC. Так что, если он сформулировал теорему Соловья так же как написано в статье, то понятно почему его не так поняли упомянутые в той же статье математики

[маткиб]

MaximKat писал(а):

Тут автор противоречит сам себе. Если неизмеримое множество явно построить нельзя, то логично, что явно построенное множество измеримо.

Он наверно имел в виду, что нельзя построить неизмеримое множество и доказать в ZF, что оно неизмеримо.

Кстати, Непейвода вовсе не идиот и не "фрик", и это общепризнанный факт, в среде мат. логиков его вроде бы уважают. Правда, может быть, он слегка помешан на конструктивизме и других извращениях.

[MaximKat]

Я понимаю, что он хотел сказать. Но если учесть, что дальше он как раз обращает внимание на разницу между "невозможно построить" и "невозможно доказать", то удивительно, что сам допускает такую же ошибку.

[маткиб]

Судя по всему, Непейвода настолько привык к конструктивистскому мышлению, что даже когда рассказывает что-то обычным ("попсовым" ) математикам, подразумевает конструктивистскую трактовку кванторов. Поэтому у него из несуществования объекта, не обладающего данным свойством, не следует, что все объекты данным свойством обладают.

[Профессор Снэйп]

маткиб писал(а):

Но из цитаты Непейводы...

Ну Вы нашли кого цитировать!

Однажды Непейвода при мне процитировал Мальцева

А. И. Мальцев писал(а):

Математика заканчивается там, где начинаются интегралы.

При этом он аж весь светился таким радостным светом изнутри, что глядя на него, невозможно было усомниться в столь великой истине.

Впрочем, он всегда светится

Тут вот недавно Brukvalub давал ссылку в теме про классификацию конечных групп. Там, кстати, очень интересная статья содержится. И в ней, в частности, сказано, что Курт Гёдель был платонистом. И для Курта Гёделя постановка вопроса об истинности в теории множеств отнюдь не была абсурдной.

Добавлено спустя 27 минут 50 секунд:

маткиб писал(а):

Кстати, Непейвода вовсе не идиот и не "фрик", и это общепризнанный факт, в среде мат. логиков его вроде бы уважают.

Я сам матлогик. Более того, из Новосибирска, как и Непейвода (хотя тот вроде бы давно уже в Москве или где-то ещё). Непейводу знаю лично, правда не сказать, что очень уж хорошо.

Мне он известен как довольно грамотный популяризатор матлогики в среде философов. И вообще, студенты-философы его гораздо лучше знают, чем студенты-математики.

Математических же работ Непейводы я не читал. В качестве автора какого-нибудь известного результата он мне неизвестен. Надо будет в ближайшее время, когда окажусь в институте, пошариться в MathSciNet и посмотреть, что он опубликовал и где (не считая, конечно, философско-математических популярностей).

[AD]

маткиб писал(а):

Цитата:

... До сих пор в работах ведущих математиков встречаются вопросы типа "Ну да, мы слышали, что гипотеза континуума неразрешима. Но на самом деле истинна она или нет?" ...

А ссылочек на такие работы никто не подбросит? Чтобы именно "до сих пор".

[shwedka]

Профессор Снэйп

Цитата:

Непейвода (хотя тот вроде бы давно уже в Москве или где-то ещё).
Математических же работ Непейводы я не читал. В качестве автора какого-нибудь известного результата он мне неизвестен. Надо будет в ближайшее время, когда окажусь в институте, пошариться в MathSciNet и посмотреть, что он опубликовал и где (не считая, конечно, философско-математических популярностей).

Я посмотрела. Он в Ижевске, держит себя корифеем, объявляется автором 150 трудов. Читает лекции по теоретическому программированию.
MathSciNet дает 34 труда, из них, вроде бы, штук 15 серьезных.

[Профессор Снэйп]

А где он, кстати, публиковался? Если у него в "Алгебре и Логике" или в "СМЖ" статьи есть (10-20 летней давности), то можно будет без проблем на них глянуть.

Добавлено спустя 30 минут 49 секунд:

Забавно. Про Непейводу даже статья в Википедии есть, как выясняется. Ну, блин... Люди себя уже в энциклопедиях пиарят. Может, нам всем тоже стоит друг про друга по статейке в Вики налобать?

Глеб Самойлов писал(а):

Да, возможно, Пуркуа Па, мы войдем в историю.
Твой и мой фотопортрет спрячут в хрестоматию...

[маткиб]

Особенно нравится вот это:

wikipedia писал(а):

Ученики являются руководителями фирм и ведущими специалистами[ИСТОЧНИК?]. Ведущие фирмы, приглашавшие их к себе, с удивлением отмечали, что их подготовка глубже, скажем, чем в МГУ и НГУ[ИСТОЧНИК?].

[Профессор Снэйп]

MaximKat писал(а):

...результат Соловья...

...он сформулировал теорему Соловья...

Вроде правильно писать "Соловея" или "Соловэя". Оригинальная фамилия пишется "Solovay", если не ошибаюсь.

Добавлено спустя 2 минуты 34 секунды:

маткиб писал(а):

Особенно нравится вот это:

wikipedia писал(а):

Ученики являются руководителями фирм и ведущими специалистами[ИСТОЧНИК?]. Ведущие фирмы, приглашавшие их к себе, с удивлением отмечали, что их подготовка глубже, скажем, чем в МГУ и НГУ[ИСТОЧНИК?].

Угу. Очень энциклопедично.

Не знаю, сам Н. Н. это писал или кто за него постарался. Но после того, как я эту статью увидел, уважение к человеку сразу упало на несколько порядков.

[MaximKat]

Все может быть. Я с ним первый раз столкнулся в обсуждаемой статье, а там используется именно "Соловья"

[shwedka]

Профессор Снэйп
Публикации (последние!!!)

Logical and algorithmic formalisms for problems of the construction of correct programs. (Russian) Programmirovanie 1999, , no. 6, 57--66

Incomplete proof structures and their application. (Russian) Logical investigations, No. 5 (Russian) (Moscow, 1997), 61--73, "Nauka", Moscow, 1998.

On a modification of semantic tableaux. (Russian) Logical investigations, No. 4 (Russian), 173--179, "Nauka", Moscow, 1997.

First steps toward a theory of unformalizable concepts. (Russian) Logical investigations, No. 1 (Russian), 34--45, "Nauka", Moscow, 1993

A bridge between constructive logic and computer programming. Images of programming. Theoret. Comput. Sci. 90 (1991), no. 1, 253--270.

First steps toward a theory of nonformalizable concepts. (Russian) Investigations in nonclassical logics (Russian) (Telavi, 1985), 54--70, "Nauka", Moscow, 1989.

Some semantic constructions of constructive logic schemes of programs. (Russian) Vychisl. Sistemy No. 129, Teor. Algoritm. i ee Prilozhen. (1989), 49--66

Constructive logical tools. II. Intuitionistic logic and constructive logics of program schemes. Soviet J. Comput. Systems Sci. 27 (1989), no. 3, 81--93 (1990); translated from Izv. Akad. Nauk SSSR Tekhn. Kibernet. 1988, , no. 2, 65--81,

Formalization of nonformalizable notions: autoproductive systems of theories. (Russian) Semiotics and information science, No. 25, 46--93, 153, Akad. Nauk SSSR, Vsesoyuz. Inst. Nauchn. i Tekhn. Inform., Moscow, 1985.

[Sonic86]

Честно говоря, я не специалист, но мне кажется, что все это на уровне бла-бла-бла. Напишу от себя как от очень ортодоксального математика.
Я не буду говорить о всем, что там не относится к математике – неохота просто.
Поражает несвязанность мыслей. Поэтому тут можно каждый отдельный момент отдельно покритиковать – все равно они несвязанны.
Про то, что логику не знают – жаль, конечно, хотелось бы большего.
По поводу невозможности построения неизмеримого множества. Честно говоря, в свое время тоже был в шоке, но потом привык. Поэтому мне все это представляется как еще один аспект спора о том, что лучше: интуитивное или конструктивное. Поэтому и ответ тот же, что и обычно в этих спорах: а кто его знает, теории-то несравнимы, нужно детальное выяснение того, что дает каждая теория и как результаты каждой теории соотносятся между собой. О том, как же строится это множество, следует смотреть историю аксиомы Цермело – математики и до него серьезно спорили на эту тему, а аксиому приняли из практических соображений. Грубо говоря, у неконструктивных объектов такое свойство: раз они не могут быть построены, то могут обладать довольно странными свойствами, но противоречия это не дает. Утверждения о них вместе с аксиомой Цермело недоказуемы, поэтому, как справедливо замечает автор, неистинны и не ложны. Их можно принимать, а можно отвергать – противоречия все равно не будет. Если я правильно понимаю интуитивистов, то они принимают за истину то из недоказуемого утверждения и его отрицания, что в логической форме имеет на первом месте квантор всеобщности – для продуктивности. Видимо, примерно это автор имеет ввиду, когда неконструктивность влечет истинность, хотя он сам к этому относится с иронией.
По поводу конструктивности и его классификации теорем существования, которые дают алгоритм, не дают, но дают описание и т. п.. 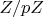Я бы хотел посмотреть на автора, как бы он в поле вычетов конструктивно доказывал существование образующей, существование единственности разложения простого числа вида $4k+1$ в сумму двух квадратов и подобных, более сложных результатов, очень бы хотел посмотреть на конструктивное доказательство теоретико-числового утверждения типа: число решений такого-то уравнения в поле вычетов $Z/pZ$ не меньше $p-2p^{1/2}$, и это – далеко не предел. Тут автор, на мой взгляд, загнул…

[ewert]

Я так понял, что Непейвода возмущается не столько континуум-гипотезой, сколько аксиомой выбора. И хотя это и одно и то же, но психологически разница всё-таки существенна. Поскольку аксиома выбора -- действительно неконструктивна. Соответственно, подвисают и завязанные на неё теоремы.

Причём случай с множеством Витали ещё безобиден. Ну какая, в самом деле, разница -- существуют неизмеримые множества или нет. Главное, что теория меры непротиворечива, и все практически мыслимые множества вроде бы измеримы.

Но вот более грустная ситуация -- например, теорема Хана-Банаха. Насколько я знаю, все её доказательства так или иначе опираются на аксиому выбора. А это означает, что теорема звучит примерно так: да, ребята, можно продолжить функционал с сохранением нормы, но вам этого продолжения -- ни в жисть и никак не найти! Ну и какой с такого утверждения прок?