Кошмар ученого

[Sicker]

Есть ли такие задачки, скажем проверить истинность какого-то утверждения о функциях и уравнениях, но аналитикой задачка явно не берется(и не ясно в принципе берется ли, допустим что не берется), а если считать численно, то параметры в задаче пробегают скажем ряд натуральных чисел от нуля до $10$ в миллионной степени, или какого-либо другого числа, которое несоизмеримо больше всего количества формул, которые могут быть написаны на бумаги чернилами или просчитаны компьютером.

[Soul Friend]

$$\sum_{n=1}^{\infty}n=-\frac{1}{12}$$

[knizhnik]

Soul Friend в сообщении #1163117 писал(а):

$\sum_1^{\infty}=-\frac{1}{12}$

После знака суммы что-то явно пропущено, да?

[Simple Fairy]

А как вы докажите, что не берется рассуждениями?
Может не совсем то, но я не представляю, как например можно проверить число Грэма из определенной задачи по теории Рамсея.

(Оффтоп)

P.S. Насколько мне известно, что если представить это число, то можно получить чёрную дыру.

-- 26.10.2016, 05:00 --

knizhnik в сообщении #1163118 писал(а):

Soul Friend в сообщении #1163117 писал(а):

$\sum_1^{\infty}=-\frac{1}{12}$

После знака суммы что-то явно пропущено, да?

Нет, просто это не обычная сумма, а суммирование по методу Рамануджана.
Конечного предела сумма не имеет и ряд расходится.

[atlakatl]

Sicker
Почему кошмар? Придумать задачу, в которой реально применяется трудновообразимое число - как число Грэма - очень интересно, познавательно и зрелищно.
А уж решить её вообще сногсшибательно.

[madschumacher]

Ну Вы бы для начала посмотрели список открытых математических проблем (хоть те же Задачи Тысячелетия). Из них, имхо, те, что Гипотеза Римана и про решения Навье-Стокса вполне удовлетворяют вопросу ТС.

[Brukvalub]

(Оффтоп)

Simple Fairy в сообщении #1163119 писал(а):

P.S. Насколько мне известно, что если представить это число, то можно получить чёрную дыру.

А если лошадь подумает про это число, то она умирает! Хомячка же это число мгновенно разрывает в клочья! Поговаривают также, что звезда Р17Н155 в созвездии Лиры превратилась в сверхновую именно потому, что сразу семеро инопланетян, живших на 4-й планете планетной системы этой звезды, одновременно подумали о числе Грэма...

[Simple Fairy]

Brukvalub в сообщении #1163132 писал(а):

(Оффтоп)

Simple Fairy в сообщении #1163119 писал(а):

P.S. Насколько мне известно, что если представить это число, то можно получить чёрную дыру.

А если лошадь подумает про это число, то она умирает! Хомячка же это число мгновенно разрывает в клочья! Поговаривают также, что звезда Р17Н155 в созвездии Лиры превратилась в сверхновую именно потому, что сразу семеро инопланетян, живших на 4-й планете планетной системы этой звезды, одновременно подумали о числе Грэма...

(Оффтоп)

Без шуток, речь шла не о какой-то псевдонаучной информации, а о том, что запись каждой цифры по крайне мере это объем Планка, масса записи данного числа и объема 'мозга' сопоставимы с черной дырой.

[madschumacher]

Simple Fairy в сообщении #1163136 писал(а):

Без шуток, речь шла не о какой-то псевдонаучной информации, а о том, что запись каждой цифры по крайне мере это объем Планка, масса записи данного числа и объема 'мозга' сопоставимы с черной дырой.

Ну для доказательства не псевдонаучности Вы могли бы привести формулы, поясняющие Ваши слова о массе. А то обычно дисклеймер про то, что высказывание не лже/псевдонаука обычно перед ней самой и следует.

[Droog_Andrey]

atlakatl в сообщении #1163120 писал(а):

Sicker
Почему кошмар? Придумать задачу, в которой реально применяется трудновообразимое число - как число Грэма - очень интересно, познавательно и зрелищно.
А уж решить её вообще сногсшибательно.

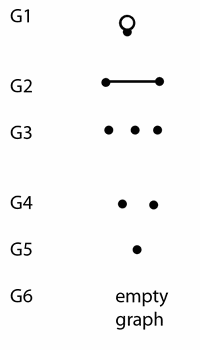
Мы строим последовательность графов $G_1, G_2, G_3, ...$, таких, что каждая вершина не более чем трёхвалентна, по следующим правилам:
1. Каждый член последовательности должен быть таким, чтобы из него нельзя было получить ни один из предыдущих членов путём удаления рёбер, удаления вершин либо стягивания рёбер.
2. Число вершин в $G_n$ не превышает $n+k$.

Пусть максимально возможная длина последовательности, построенной по этим правилам, равна $SCG(k)$. Например, $SCG(0) = 6$:


Число $SCG(3)$ оказывается весьма велико.

[Someone]

$G_1$ — не граф, а псевдограф.

Ф. Харари. Теория графов. "Мир", Москва, 1973.

Определения можно найти в главе 2. Впрочем, там же он сетует на то, что в теории графов каждый автор использует собственную терминологию.

[Droog_Andrey]

Someone, конкретно в этой задаче разрешены петли и кратные рёбра :)

[Someone]

Именно это и называется словом "псевдограф".

[Droog_Andrey]

А в зарубежной литературе "мультиграф". По поводу петель как-то толком не договорились.

(Оффтоп)

Это как со щёлочноземельными металлами в химии: у нас они начинаются с кальция, а за рубежом и магний, и даже бериллий туда относят.

Конкретно эту задачу придумал Фридман, в её контексте привычнее графы без петель и кратных рёбер называть простыми графами и соответствующую функцию обозначать $SSCG(n)$ (от слов simple subcubic graph).

[Someone]

Droog_Andrey в сообщении #1164706 писал(а):

А в зарубежной литературе "мультиграф".

Книга Харари — это как раз "зарубежная литература". У него мультиграф может быть с кратными рёбрами, но заведомо без петель.

Но Харари прямо говорит, что каждый автор в теории графов использует собственную терминологию. Так что я не вижу смысла в продожении обсуждения терминологии теории графов. Я просто проинформировал о существующей ситуации.